
科目: 来源: 题型:
【题目】据《人民网》报道,“美国国家航空航天局( NASA)发文称,相比20年前世界变得更绿色了,卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的420/0来自于植树造林,下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
按造林方式分 | ||||||
地区 | 造林总面积 | 人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 |
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 221117 | 15376 | 133 |
重庆 | 226333 | 100600 | 、 62400 | 63333 | ||
陕西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012、 | 4000 | 3999 | 1053 | |
(1)请根据上述数据,分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(2)在这十个地区中,任选一个地区,求该地区人工造林面积与造林总面积的比值不足50%的概率是多少?
(3)从上表新封山育林面积超过十万公顷的地区中,任选两个地区,求至少有一个地区退化林修复面积超过五万公顷的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
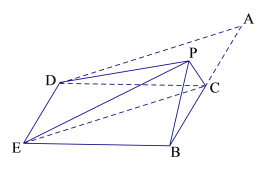
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】十九世纪末:法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”“随机端点”“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设![]() 为圆
为圆![]() 上一个定点,在圆周上随机取一点
上一个定点,在圆周上随机取一点![]() ,连接
,连接![]() ,所得弦长
,所得弦长![]() 大于圆
大于圆![]() 的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且f(x+2)=f(2-x),当x∈[-2,0]时,f(x)= ,则在区间(-2,6)上关于x的方程f(x)-log8(x+2)=0的解的个数为( )
,则在区间(-2,6)上关于x的方程f(x)-log8(x+2)=0的解的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目: 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(1+x)t﹣1的定义域为(﹣1,+∞),其中实数t满足t≠0且t≠1.直线l:y=g(x)是f(x)的图象在x=0处的切线.
(1)求l的方程:y=g(x);
(2)若f(x)≥g(x)恒成立,试确定t的取值范围;
(3)若a1,a2∈(0,1),求证: ![]() .注:当α为实数时,有求导公式(xα)′=αxα﹣1.
.注:当α为实数时,有求导公式(xα)′=αxα﹣1.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知O为坐标原点,过点M(1,0)的直线l与抛物线C:y2=2px(p>0)交于A,B两点,且![]() .
.
(1)求抛物线C的方程;
(2)过点M作直线l'⊥l交抛物线C于两点,记△OAB,△OPQ的面积分别为S1,S2,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠DAB=90°AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC![]() ,E是线段AB的中点.
,E是线段AB的中点.
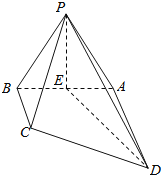
(1)求证:PE⊥CD;
(2)求PC与平面PDE所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数f(x)![]() (c≠0),其图象的对称中心为(
(c≠0),其图象的对称中心为(![]() ,
,![]() ),现已知f(x)
),现已知f(x)![]() ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f(![]() )(n∈N+),则此数列前2020项的和为_____.
)(n∈N+),则此数列前2020项的和为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() ,以原点
,以原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(1)若曲线C1方程中的参数是α,且C1与C2有且只有一个公共点,求C1的普通方程;
(2)已知点A(0,1),若曲线C1方程中的参数是t,0<α<π,且C1与C2相交于P,Q两个不同点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com