【题目】已知椭圆：的左顶点为，右焦点为，斜率为1的直线与椭圆交于，两点，且，其中为坐标原点.

（1）求椭圆的标准方程；

（2）设过点且与直线平行的直线与椭圆交于，两点，若点满足，且与椭圆的另一个交点为，求的值.

【题目】在四棱锥P﹣ABCD中，△PAB是边长为2的等边三角形，底面ABCD为直角梯形，AB∥CD，AB⊥BC，BC＝CD＝1，PD.

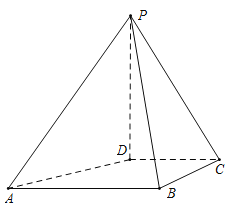
（1）证明：AB⊥PD.

（2）求二面角A﹣PB﹣C的余弦值.

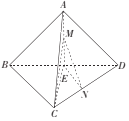
【题目】如图，在三棱锥A﹣BCD中，点E在BD上，EA＝EB＝EC＝ED，BDCD，△ACD为正三角形，点M，N分别在AE，CD上运动（不含端点），且AM＝CN，则当四面体C﹣EMN的体积取得最大值时，三棱锥A﹣BCD的外接球的表面积为_____.

（1）从空气质量指数属于[0，50]，（50，100]的天数中任取3天，求这3天中空气质量至少有2天为优的概率；

（2）已知某企业每天因空气质量造成的经济损失y（单位：元）与空气质量指数x的关系式为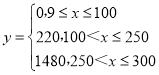，假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为.9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.

（i）记该企业9月每天因空气质量造成的经济损失为X元，求X的分布列；

（ii）试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元？说明你的理由.

【题目】设函数，，其中，为正实数.

（1）若的图象总在函数的图象的下方，求实数的取值范围；

（2）设，证明：对任意，都有.

【题目】将函数f（x）＝3sin（﹣3x）﹣2的图象向右平移个单位长度得到函数g（x）的图象，若g（x）在区间[，θ]上的最大值为1，则θ的最小值为（ ）

A.B.C.D.

A.56383B.57171C.59189D.61242

【题目】已知函数.

（1）若，求的单调区间；

（2）若是的唯一极值点，求的取值范围.

【题目】如图，正三棱柱的所有棱长都为，是的中点，在边上，.

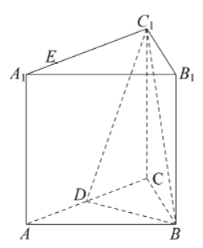
（1）证明：平面平面；

（2）若是侧面内的动点，且平面.

①在答题卡中作出点的轨迹，并说明轨迹的形状（不需要说明理由）；

②求三棱锥的体积.

【题目】新冠肺炎疫情期间，为了减少外出聚集，“线上买菜”受追捧.某电商平台在地区随机抽取了位居民进行调研，获得了他们每个人近七天“线上买菜”消费总金额（单位：元），整理得到如图所示频率分布直方图.

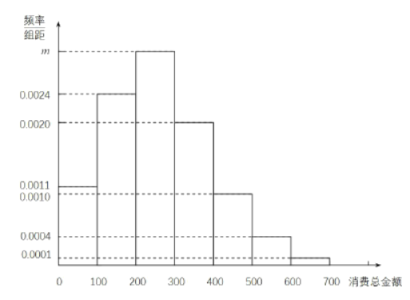
（1）求的值；

（2）从“线上买菜”消费总金额不低于元的被调研居民中，随机抽取位给予奖品，求这位“线上买菜”消费总金额均低于元的概率；

（3）若地区有万居民，该平台为了促进消费，拟对消费总金额不到平均水平一半的居民投放每人元的电子补贴.假设每组中的数据用该组区间的中点值代替，试根据上述频率分布直方图，估计该平台在地区拟投放的电子补贴总金额.