
| A. | g△tcosθ1 | B. | g△ttanθ1 | ||
| C. | $\frac{g△t}{tan{θ}_{2}-tan{θ}_{1}}$ | D. | $\frac{g△t}{cos{θ}_{1}-cos{θ}_{2}}$ |
分析 将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动两个分力,作出t秒末和t+t0秒末速度的分解图.研究竖直方向的速度,分别用初速度表示,再由速度公式求出初速度.
解答 解:设小球的初速度为${v}_{0}^{\;}$
ts末竖直分速度${v}_{1y}^{\;}=gt$
ts末速度分解如图所示
由几何关系得${v}_{1y}^{\;}={v}_{0}^{\;}tan{θ}_{1}^{\;}$
(t+△t)s末速度分解如图: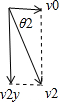
由几何关系得${v}_{2y}^{\;}={v}_{0}^{\;}tan{θ}_{2}^{\;}$
根据速度公式:${v}_{2y}^{\;}={v}_{1y}^{\;}+g•△t$
代入数据:${v}_{0}^{\;}tan{θ}_{2}^{\;}={v}_{0}^{\;}tan{θ}_{1}^{\;}+g•△t$
解得:${v}_{0}^{\;}=\frac{g△t}{tan{θ}_{2}^{\;}-tan{θ}_{1}^{\;}}$
故选:C
点评 本题本题考查对平抛运动的处理能力,关键是作出速度的分解图,对速度进行分解处理.注意必须学会作草图,并画出实际运动过程才可以知道答案


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:多选题
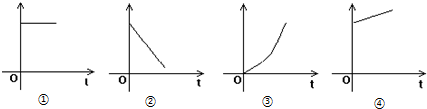
| A. | 图①是加速度--时间图象 | B. | 图②是加速度--时间图象 | ||
| C. | 图③是位移--时间图象 | D. | 图④是速度--时间图象 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
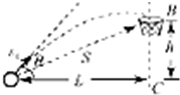 一个运动员投篮,投射角为θ,出手点O与篮圈的高度差为h,水平距离为L.为了将球投入篮中,则出手速度v0应为( )
一个运动员投篮,投射角为θ,出手点O与篮圈的高度差为h,水平距离为L.为了将球投入篮中,则出手速度v0应为( )| A. | $\sqrt{\frac{g}{2(Ltanθ-h)}}$ | B. | $\frac{L}{cosθ}$$\sqrt{\frac{g}{2(Ltanθ-h)}}$ | C. | $\sqrt{\frac{g}{Ltanθ-h}}$ | D. | $\frac{L}{cosθ}$$\sqrt{\frac{2(Ltanθ-h)}{g}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
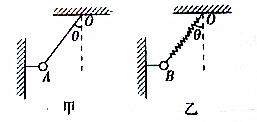
 如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,AB间的距离x=4m,B、C分别为半圆轨道的最低点和最高点,半圆轨道半径R=0.4m.一个质量m=0.1kg的小物体P在A点以一定的初速度向B点运动,后滑上半圆轨道,并恰好能经过C点.已知小物体P与水平轨道间的动摩擦因数μ=0.2,g取10m/s2.求
如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,AB间的距离x=4m,B、C分别为半圆轨道的最低点和最高点,半圆轨道半径R=0.4m.一个质量m=0.1kg的小物体P在A点以一定的初速度向B点运动,后滑上半圆轨道,并恰好能经过C点.已知小物体P与水平轨道间的动摩擦因数μ=0.2,g取10m/s2.求查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 某游乐场水上滑梯的简化模型如图所示:倾角θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7m,BC长d=2m,端点C距水面的高度h=1m.质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.1.已知cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点,g取10m/s2.求:
某游乐场水上滑梯的简化模型如图所示:倾角θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7m,BC长d=2m,端点C距水面的高度h=1m.质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.1.已知cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点,g取10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com