
| A. | $\sqrt{\frac{k}{n}}M$ | B. | $\frac{{n}^{3}}{{k}^{2}}M$ | C. | $\frac{n}{k}M$ | D. | $\frac{{n}^{3}}{{k}^{3}}M$ |
分析 双星靠相互间的万有引力提供向心力,具有相同的角速度,根据牛顿第二定律和向心力公式,分别对两星进行列式,求解出总质量的表达式进行分析.
解答 解:设m1的轨道半径为R1,m2的轨道半径为R2.两星之间的距离为L.
由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同.
由向心力公式可得:对m1:$\frac{{G{m_1}{m_2}}}{L^2}={m_1}\frac{{4{π^2}}}{T^2}{R_1}$…①
对m2:$\frac{{G{m_1}{m_2}}}{L^2}={m_2}\frac{{4{π^2}}}{T^2}{R_2}$…②
又因为R1+R2=L,m1+m2=M
由①②式可得:M=$\frac{4{π}^{2}{L}^{3}}{G{T}^{2}}$
经过一段时间演化后,两星做圆周运动的周期变为原来的k倍,两星之间的距离变为原来的n倍,故:
M′=$\frac{4{π}^{2}{{n}^{3}L}^{3}}{G{{k}^{2}T}^{2}}$
故M′=$\frac{{n}^{3}}{{k}^{2}}M$
故选:B
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度,能运用万有引力提供向心力进行解题.


科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
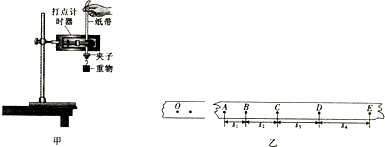
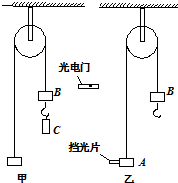 如图甲所示的装置叫做阿物伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创新的一种著名力学实验装置,用来研究匀变速直线运动的规律,某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿物伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创新的一种著名力学实验装置,用来研究匀变速直线运动的规律,某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
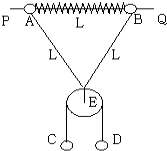 如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.用手水平托住D球并保持D球静止状态,此时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)求:
如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.用手水平托住D球并保持D球静止状态,此时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 质点是不存在的,引入这概念没有意义 | |
| B. | 物体在运动过程中,路程总等于位移的大小 | |
| C. | 加速度减小,速度一定也减小 | |
| D. | 速度变化越快,加速度越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 电动公交车主要是指纯电动公交车,全部使用电能行驶,该类公交车噪音小,行驶稳定性高,并且实现零排放.如图所示,某电动公交车做匀加速直线运动,在10s内,速度由0增加到20m/s,则该电动公交车的加速度为( )
电动公交车主要是指纯电动公交车,全部使用电能行驶,该类公交车噪音小,行驶稳定性高,并且实现零排放.如图所示,某电动公交车做匀加速直线运动,在10s内,速度由0增加到20m/s,则该电动公交车的加速度为( )| A. | 0.5m/s2 | B. | 1m/s2 | C. | 2m/s2 | D. | 4m/s2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com