
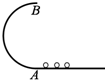
 如图所示,半径为R的光滑半圆形轨道和光滑水平轨道相切,三个小球1、2、3沿水平轨道分别以速度v1=2$\sqrt{gR}$、v2=3$\sqrt{gR}$、v3=4$\sqrt{gR}$水平向左冲上半圆形轨道,g为重力加速度,下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是( )
如图所示,半径为R的光滑半圆形轨道和光滑水平轨道相切,三个小球1、2、3沿水平轨道分别以速度v1=2$\sqrt{gR}$、v2=3$\sqrt{gR}$、v3=4$\sqrt{gR}$水平向左冲上半圆形轨道,g为重力加速度,下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是( )| A. | 三个小球离开轨道后均做平抛运动 | |
| B. | 小球2和小球3的落点到A点的距离之比为$\sqrt{5}$:2$\sqrt{3}$ | |
| C. | 小球1和小球2做平抛运动的时间之比为1:1 | |
| D. | 小球2和小球3做平抛运动的时间之比为1:1 |
分析 先求出小球通过最高点时的临界速度,再分析三个小球能否到达最高点.若能通过最高点就能做平抛运动,再由平抛运动的规律分析水平距离和时间之比.
解答 解:A、设小球恰好通过最高点时的速度为v,此时由重力提供向心力,则 mg=m$\frac{{v}^{2}}{R}$,得 v=$\sqrt{gR}$
设小球能通过最高点时在轨道最低点时最小速度为v′,由机械能守恒定律得 2mgR+$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}mv{′}^{2}$,得 v′=$\sqrt{5gR}$
由于v1=2$\sqrt{gR}$<v′,所以小球1不能到达轨道最高点,也就不能做平抛运动,故A错误.
BCD、小球2和小球3离开轨道后做平抛运动,由2R=$\frac{1}{2}g{t}^{2}$得 t=2$\sqrt{\frac{R}{g}}$,则得:小球2和小球3做平抛运动的时间之比为1:1.
设小球2和小球3通过最高点时的速度分别为v2′和v3′.根据机械能守恒定律得:
2mgR+$\frac{1}{2}$mv22=$\frac{1}{2}$mv2′2;2mgR+$\frac{1}{2}$mv32=$\frac{1}{2}$mv3′2;
解得 v2′=$\sqrt{5gR}$,v3′=$2\sqrt{3gR}$
由平抛运动规律得:水平距离为 x=v0t,t相等,则小球2和小球3的落点到A点的距离之比为$\sqrt{5}$:2$\sqrt{3}$.
小球1做的不是平抛运动,则小球1和小球2做平抛运动的时间之比不是1:1,故BD正确,C错误.
故选:BD
点评 解决本题的关键要掌握圆周运动最高点的临界条件,明确小球离开轨道后做平抛运动,应用平抛知识、机械能守恒定律结合解题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中物理 来源: 题型:选择题
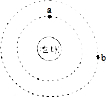 如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )| A. | lg($\frac{{v}_{1}}{{v}_{2}}$)=$\frac{1}{3}$lg($\frac{{T}_{1}}{{T}_{2}}$) | B. | lg($\frac{{v}_{1}}{{v}_{2}}$)=3lg($\frac{{T}_{1}}{{T}_{2}}$) | ||
| C. | lg($\frac{{v}_{1}}{{v}_{2}}$)=$\frac{1}{3}$lg($\frac{{T}_{2}}{{T}_{1}}$) | D. | lg($\frac{{v}_{1}}{{v}_{2}}$)=3lg($\frac{{T}_{2}}{{T}_{1}}$) |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 太空中的物体处于完全失重状态,无法用天平直接测量其质量.为测定一小球的质量,将小球放在带有压力传感器的小车上,小车在电机带动下向右做匀加速运动,并通过速度传感器测出挡光片Ⅰ、挡光片Ⅱ经过速度传感器时的速度.通过计算机程序显示出小球的质量.
太空中的物体处于完全失重状态,无法用天平直接测量其质量.为测定一小球的质量,将小球放在带有压力传感器的小车上,小车在电机带动下向右做匀加速运动,并通过速度传感器测出挡光片Ⅰ、挡光片Ⅱ经过速度传感器时的速度.通过计算机程序显示出小球的质量.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
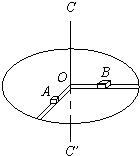 半径为R的水平圆台,可绕通过圆心O的竖直光滑细轴CC′转动,如图所示,圆台上沿相互垂直的两个半径方向刻有凹槽,质量为mA的物体A放在一个槽内,物体A与槽底间的动摩擦因数为μ,质量为mB的物体B放在另一个槽内,此槽是光滑的.AB间用一长为l(l<R)且不可伸长的轻绳绕过细轴相连.已知圆台做匀速转动,且A、B两物体相对圆台不动(A、B两物体可视为质点,物体的最大静摩擦力近似等于滑动摩擦力).下列叙述正确的是( )
半径为R的水平圆台,可绕通过圆心O的竖直光滑细轴CC′转动,如图所示,圆台上沿相互垂直的两个半径方向刻有凹槽,质量为mA的物体A放在一个槽内,物体A与槽底间的动摩擦因数为μ,质量为mB的物体B放在另一个槽内,此槽是光滑的.AB间用一长为l(l<R)且不可伸长的轻绳绕过细轴相连.已知圆台做匀速转动,且A、B两物体相对圆台不动(A、B两物体可视为质点,物体的最大静摩擦力近似等于滑动摩擦力).下列叙述正确的是( )| A. | 当圆台转动的角速度为ω0,OA的长度为l1时,A的向心力为FA=mAω02R | |
| B. | 若lOA=$\frac{m_B}{{{m_A}+{m_B}}}$l,则无论圆台转动的角速度为多大,物体A和槽之间始终没有摩擦力 | |
| C. | lOA=$\frac{{0.8{m_B}}}{{{m_A}+{m_B}}}$l,圆台转动的角速度ω过大时,A必将远离O点 | |
| D. | 若lOA=$\frac{{0.9{m_B}}}{{{m_A}+{m_B}}}$l,圆台转动的角速度ω过大时,B必将远离O点 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
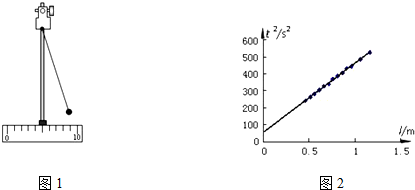
 某实验小组用一只弹簧秤和一个量角器等器材验证力的平行四边形定则,设计了如图所示的实验装置,固定在竖直木板上的量角器的直边水平,橡皮筋的一端固定于量角器的圆心O的正上方A处,另一端系绳套1和绳套2.主要实验步骤如下:
某实验小组用一只弹簧秤和一个量角器等器材验证力的平行四边形定则,设计了如图所示的实验装置,固定在竖直木板上的量角器的直边水平,橡皮筋的一端固定于量角器的圆心O的正上方A处,另一端系绳套1和绳套2.主要实验步骤如下:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 在做“研究匀变速直线运动”的实验时,某同学得到一条用打点计时器打下的纸带,如图所示,并在其上取了A、B、C、D、E、F等6个计数点,(每相邻两个计数点间还有4个打点计时器打下的点,本图中没有画出)打点计时器接的是“220V、50Hz”的交变电流.如图1,他把一把毫米刻度尺放在纸带上,其零刻度和计数点A对齐,求:
在做“研究匀变速直线运动”的实验时,某同学得到一条用打点计时器打下的纸带,如图所示,并在其上取了A、B、C、D、E、F等6个计数点,(每相邻两个计数点间还有4个打点计时器打下的点,本图中没有画出)打点计时器接的是“220V、50Hz”的交变电流.如图1,他把一把毫米刻度尺放在纸带上,其零刻度和计数点A对齐,求:| vB | vC | vD | vE |
| 0.12m/s | 0.16m/s | 0.25m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一小木块(可视为质点)沿倾角为37°的斜面从斜面底端以4m/s的初速度滑上斜面,已知斜面与小木块间的动摩擦因数为0.25,规定木块初始位置的重力势能为零,求木块的重力势能等于动能时距斜面底端的高度(sin37°=0.6,cos37°=0.8,g=10m/s2).
如图所示,一小木块(可视为质点)沿倾角为37°的斜面从斜面底端以4m/s的初速度滑上斜面,已知斜面与小木块间的动摩擦因数为0.25,规定木块初始位置的重力势能为零,求木块的重力势能等于动能时距斜面底端的高度(sin37°=0.6,cos37°=0.8,g=10m/s2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com