
分析 根据地球表面处重力等于万有引力和卫星受到的万有引力等于向心力,即$G\frac{Mm}{{r}^{2}}=ma=m\frac{{v}^{2}}{r}=m\frac{{4π}^{2}r}{{T}^{2}}$列式即可求解.
解答 解:根据卫星受到的万有引力等于向心力得:
$G\frac{Mm}{{(R+R)}^{2}}=m\frac{{v}^{2}}{2R}$
地球表面处重力等于万有引力$G\frac{Mm}{{R}^{2}}=mg$
解得:v=$\sqrt{\frac{gR}{2}}$
T=$\frac{2π(2R)}{v}=\frac{4πR}{\sqrt{\frac{gR}{2}}}=4π\sqrt{\frac{2R}{g}}$
根据$G\frac{Mm}{{(R+R)}^{2}}=ma$及$G\frac{Mm}{{R}^{2}}=mg$可知:
a=$\frac{1}{4}g$
根据ω=$\frac{2π}{T}$=$\frac{1}{2}\sqrt{\frac{g}{2R}}$
故答案为:$\sqrt{\frac{gR}{2}}$;$\frac{1}{2}\sqrt{\frac{g}{2R}}$;$\frac{1}{4}g$;$4π\sqrt{\frac{2R}{g}}$
点评 解决本题的关键是掌握万有引力提供向心力,即$G\frac{Mm}{{r}^{2}}=ma=m\frac{{v}^{2}}{r}=m\frac{{4π}^{2}r}{{T}^{2}}$,该题难度不大,属于基础题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中物理 来源: 题型:选择题
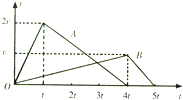 质量相等的A、B两物体(均可视为质点)放在同一水平面上,分别受到水平恒力F1、F2的作用,同时由静止开始从同一位置出发沿相同方向做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时分别撤去F1和F2,以后物体继续做匀减速运动直至停止.两物体速度随时间变化的图象如图所示,对于上述过程下列说法中正确的是( )
质量相等的A、B两物体(均可视为质点)放在同一水平面上,分别受到水平恒力F1、F2的作用,同时由静止开始从同一位置出发沿相同方向做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时分别撤去F1和F2,以后物体继续做匀减速运动直至停止.两物体速度随时间变化的图象如图所示,对于上述过程下列说法中正确的是( )| A. | 物体A、B的位移大小之比是6:5 | |
| B. | 两物体运动的全过程,合外力对A物体做的功多 | |
| C. | 在2t0和3t0间的某一时刻B追上A | |
| D. | 两物体运动过程中,A一直在B的前面 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{V}_{1}+{V}_{2}}{2}$ | B. | $\frac{{V}_{1}×{V}_{2}}{{V}_{1}+{V}_{2}}$ | C. | $\frac{{V}_{1}×{V}_{2}}{2({V}_{1}+{V}_{2})}$ | D. | $\frac{2{V}_{1}×{V}_{2}}{{V}_{1}+{V}_{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,A、B、C三个物体用轻绳经过滑轮连接,物体A、B的速度向下,大小均为v,则物体C的速度大小为( )
如图,A、B、C三个物体用轻绳经过滑轮连接,物体A、B的速度向下,大小均为v,则物体C的速度大小为( )| A. | 2vcosθ | B. | vcosθ | C. | $\frac{2v}{cosθ}$ | D. | $\frac{v}{cosθ}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 竖直分速度等于水平分速度 | B. | 运动的位移$\frac{{\sqrt{2}{v_0}^2}}{g}$ | ||
| C. | 运动时间为$\frac{{2{v_0}}}{g}$ | D. | 瞬时速度为$\sqrt{5}{v_0}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 与卫星的质量无关 | B. | 与卫星轨道半径的$\frac{3}{2}$次方有关 | ||
| C. | 与卫星的运动速度成正比 | D. | 与行星质量M的平方根成正比 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 运动的固体具有动能 | |
| B. | 运动的液体具有动能 | |
| C. | 运动的气体不一定具有动能 | |
| D. | 固体、液体、气体都是物体,只要它们运动,就具有动能 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 20m | B. | 40m | C. | 60m | D. | 80m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com