
 长为L质量为M的木板A静止在光滑的水平桌面上,有一质量为m的小木块B以水平速度V0恰好落在木板A的左端,如图所示,木块B与木块A间的摩擦系数为μ,木块B可视为质点,试求:
长为L质量为M的木板A静止在光滑的水平桌面上,有一质量为m的小木块B以水平速度V0恰好落在木板A的左端,如图所示,木块B与木块A间的摩擦系数为μ,木块B可视为质点,试求:分析 (1)对木块和木板进行受力分析,根据牛顿第二定律即可求解木块B和木板A的加速度大小和方向;
(2)木块和木板都向右运动,木块做减速运动,木板做加速度运动,根据运动学公式求得相对于A速度
(3)木板和木块构成的系统所受到的合外力为零,因而总动量守恒,根据动量守恒定律和能量守恒定律结合求解.
解答 解:(1)木块和木板相对滑动,受到滑动摩擦力,根据牛顿第二定律得:
对于木块B:aB=$\frac{f}{m}=\frac{μmg}{m}$=μg,方向水平向左;
对于木板A:aA=$\frac{f}{M}=\frac{μmg}{M}$,方向水平向右;
(2)设经过时间t运动到A得终点,则${x}_{B}={v}_{0}t-\frac{1}{2}{a}_{B}{t}^{2}$
${x}_{A}=\frac{1}{2}{a}_{A}{t}^{2}$
$\frac{L}{2}={x}_{B}-{x}_{A}$
此时B的速度为vB=v0-aBt
A的速度为vA=aAt
相对速度为△v=vB-vA
联立解得△v=$\sqrt{{v}_{0}^{2}-(μg-\frac{μmg}{M})L}$
(3)B恰好到达A的右端不落下来时两者速度相同,设为v.
木板和木块构成的系统所受到的合外力为零,因而总动量守恒,则有:(M+m)v=mv0
解得 v=$\frac{m{v}_{0}}{M+m}$
根据系统的能量守恒得:μmgL=$\frac{1}{2}{mv}_{0}^{2}-\frac{1}{2}(M+m){v}^{2}$
解得:v0=$\sqrt{\frac{2μ(M+m)gL}{M}}$
答:
(1)A的加速度为$\frac{μmg}{M}$,方向水平向右;B的加速度是μg,方向水平向左;
(2)当B运动到A长度的中点时,相对于A的速度是$\sqrt{{v}_{0}^{2}-(μg-\frac{μmg}{M})L}$
(3)如果最后B恰好到达A的右端不落下来,则v0的值应是$\sqrt{\frac{2μ(M+m)gL}{M}}$.
点评 本题考查了牛顿第二定律、动量守恒定律和运动学公式的综合运用,关键理清放上木块后木板和木块的运动情况,抓住临界状态,结合牛顿第二定律和运动学公式进行求解或动量守恒和能量守恒结合解答.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中物理 来源: 题型:选择题
 如图所示,三个完全相同的物体a、b、c叠放在粗糙水平桌面上,a的左端通过一根轻绳与质量m=3$\sqrt{3}$kg的小球相连,小球静止在固定的光滑半球形器皿中,在半球形器皿中的绳与水平方向的夹角为60°,且半球形器皿边沿与物体a间的轻绳水平.水平向右的力F=30N作用在b上,三个物体保持静止状态.取g=10m/s2,下列说法正确的是( )
如图所示,三个完全相同的物体a、b、c叠放在粗糙水平桌面上,a的左端通过一根轻绳与质量m=3$\sqrt{3}$kg的小球相连,小球静止在固定的光滑半球形器皿中,在半球形器皿中的绳与水平方向的夹角为60°,且半球形器皿边沿与物体a间的轻绳水平.水平向右的力F=30N作用在b上,三个物体保持静止状态.取g=10m/s2,下列说法正确的是( )| A. | 物体b受到物体a施加的一个大小为30N的静摩擦力,方向水平向右 | |
| B. | 桌面对物体a的摩擦力大小为0 | |
| C. | 物体c受到物体b施加的大小为30N的静摩擦力,方向水平向右 | |
| D. | 撤去力F的瞬间,三个物体一定会获得向左的加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 一定做匀变速运动,加速度大小可能等于重力加速度的大小 | |
| B. | 一定做匀变速直线运动,加速度大小可能是5 m/s2 | |
| C. | 可能做匀减速直线运动,加速度大小是1.5 m/s2 | |
| D. | 可能做匀速圆周运动,向心加速度大小是6 m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
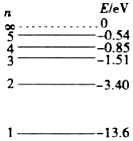 按照玻尔的理论,氢原子的能级是氢原子处于各个定态时的能量值,它包括氢原子系统的电势能和电子在轨道上运动的动能,能级图如图所示.当大量氢原子从n=4的能级向低能级跃迁时,下列说法正确的是( )
按照玻尔的理论,氢原子的能级是氢原子处于各个定态时的能量值,它包括氢原子系统的电势能和电子在轨道上运动的动能,能级图如图所示.当大量氢原子从n=4的能级向低能级跃迁时,下列说法正确的是( )| A. | 电子的动能增加,氢原子系统的总能量增加 | |
| B. | 氢原子系统的电势能减小,总能量减少 | |
| C. | 氢原子可能辐射4种不同波长的光 | |
| D. | 从n=4到n=1发出的光的波长最长 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在固定斜面上放置一物块,若在物块上再施加一个竖直向下的恒力F,则( )
如图所示,在固定斜面上放置一物块,若在物块上再施加一个竖直向下的恒力F,则( )| A. | 若原来物体匀速下滑,物块仍然匀速下滑 | |
| B. | 若原来物块加速下滑,则物体下滑的加速度更大 | |
| C. | 若原来物体匀速下滑,物体将减速下滑 | |
| D. | 若原来物块加速下滑,则物体可能加速下滑 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
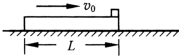 如图所示,一木板置于光滑的水平面上,可视为质点的滑块置于木板的右侧,滑块与木板之间的动摩擦因数为μ=0.2.木板的质量为M=4kg,滑块的质量m=1kg.一开始滑块静止,木板以初速度v0=10m/s向右运动,滑块恰好不从木板上掉下来,取g=10m/s2,试求:
如图所示,一木板置于光滑的水平面上,可视为质点的滑块置于木板的右侧,滑块与木板之间的动摩擦因数为μ=0.2.木板的质量为M=4kg,滑块的质量m=1kg.一开始滑块静止,木板以初速度v0=10m/s向右运动,滑块恰好不从木板上掉下来,取g=10m/s2,试求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 小汽车越壕沟比赛项目中驾驶员驾驶汽车从较高的平台上水平飞出,在空中运动一段时间后成功越过壕沟,在地面上滑行一段距离后停止.一频闪照相机记录了汽车在空中的部分位置和地面上运动至停下的位置,摄影师将其按比例印在同一张有正方形方格的照片上,如图所示.已知车长3.6m,相邻两次曝光时间相等,汽车飞离平台立即关闭发动机.图中最后两张照片有重叠不太清晰,若忽略空气阻力,取g=10m/s2,由图可知平台离地面的高度为11.25m.若汽车着地瞬间竖直分速度立即减为零,水平分速度不受影响,则汽车与水平地面间的动摩擦因数为0.67.(保留两位小数)
小汽车越壕沟比赛项目中驾驶员驾驶汽车从较高的平台上水平飞出,在空中运动一段时间后成功越过壕沟,在地面上滑行一段距离后停止.一频闪照相机记录了汽车在空中的部分位置和地面上运动至停下的位置,摄影师将其按比例印在同一张有正方形方格的照片上,如图所示.已知车长3.6m,相邻两次曝光时间相等,汽车飞离平台立即关闭发动机.图中最后两张照片有重叠不太清晰,若忽略空气阻力,取g=10m/s2,由图可知平台离地面的高度为11.25m.若汽车着地瞬间竖直分速度立即减为零,水平分速度不受影响,则汽车与水平地面间的动摩擦因数为0.67.(保留两位小数)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 气体温度每升高1 K所吸收的热量与气体经历的过程有关 | |
| B. | 悬浮在液体中的微粒越小,受到液体分子的撞击就越容易平衡 | |
| C. | 当分子间作用力表现为引力时,分子间的距离越大,分子势能越小 | |
| D. | PM 2.5的运动轨迹只是由大量空气分子对PM 2.5无规则碰撞的不平衡和气流的运动决定的 | |
| E. | 热量能够自发地从高温物体传递到低温物体,但不能自发地从低温物体传递到高温物体 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一物体从t=0开始做直线运动,其速度-时间图象如图所示,求:
一物体从t=0开始做直线运动,其速度-时间图象如图所示,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com