
渭南市崇宁中学3月月考试题
高三数学(理科)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设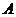 =
=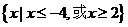 ,
,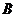 =
= ,则
,则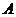

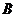 =
=
A.[2,4] B. [-2,2] C.[-2,4] D.[-4,4]
2.已知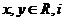 为虚数单位,且
为虚数单位,且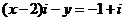 ,则
,则 的值为( )
的值为( )
A.4
B.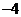 C.
C.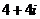 D.
D.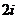
3.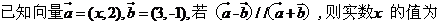
A. -12
B.
5.同时具有性质:“①最小正周期是 ②图像关于直线
②图像关于直线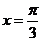 对称③在
对称③在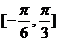 上是增函数”的一个函数是
上是增函数”的一个函数是
A.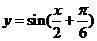 B.
B.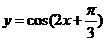

C.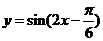 D.
D.
6.抛物线 的准线与双曲线
的准线与双曲线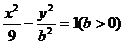 的左准线重合,则此双曲线的渐近线方程是( )
的左准线重合,则此双曲线的渐近线方程是( )
A. B.
B.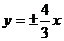 C.
C.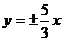 D.
D.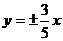
7已知函数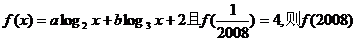 的值为
的值为
A.-4 B.
8.在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,请问实验顺序的编排方法共有
A.24种 B.48种 C.96种 D.144种
9.已知函数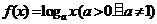 满足
满足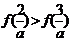 ,则
,则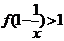 的解是( )
的解是( )
A.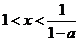 B.
B.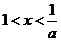 C.
C.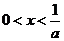 D.
D.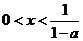
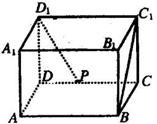 10.如右图,在正方体
10.如右图,在正方体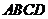 -
-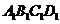 中,
中,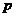 为
为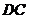 的中点,
的中点, 则
则
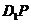 与
与 所在直线所成
所在直线所成 角的余弦值等于
角的余弦值等于
A.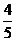 B.
B.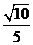 C.
C.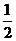 D.
D.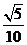

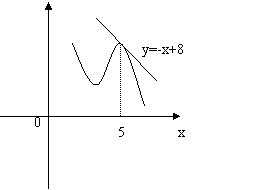 11.若
11.若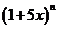 的展开式中各项系数之和为
的展开式中各项系数之和为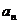 ,
, 的展开式中各项的二项式系数之和为
的展开式中各项的二项式系数之和为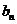 ,则
,则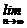
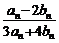 的值是
的值是
A.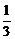 B.
B.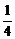 C.1 D.-
C.1 D.-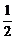
12.如图,函数的图像在P点处的切线方程是y=-x+8,
若点P的横坐标是5,则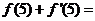 ( )
( )
A.
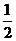 B.
B.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡中对应题号后的横线上。
13.已知点P(x,y)在不等式组 表示的平面区域内运动,则
表示的平面区域内运动,则 的取值范围是___________.
的取值范围是___________.
14.已知函数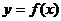 是奇函数,则当
是奇函数,则当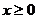 时,
时, ,设
,设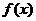 的反函数是
的反函数是 ,则
,则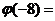 .
.
15.数列1,1,2,1,1,3,1,1,1,4,1,1,1,1,5,…,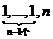 ,…的第2008项为___________,前2008项的和为___________.
,…的第2008项为___________,前2008项的和为___________.
16.在数列{an}中,都有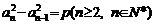 ( p为常数),则称{an}为“等方差数列”。下列是对“等方差数列”的判断:
( p为常数),则称{an}为“等方差数列”。下列是对“等方差数列”的判断:
⑴数列{an}是等方差数列,则数列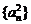 是等差数列;
是等差数列;
⑵数列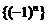 是等方差数列;
是等方差数列;
⑶若数列{an}既是等方差数列,又是等差数列,则该数列必为常数列;
⑷若数列{an}是等方差数列,则数列{akn}( k为常数,k∈N*)也是等方差数列,则正确命题序号为______。
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
 为△ABC的内角A.B.C的对边,
为△ABC的内角A.B.C的对边, ,且
,且 与
与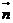 的夹角为
的夹角为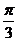 。
。
(I)求角C;
(Ⅱ)已知 ,△ABC的面积
,△ABC的面积 ,求
,求 .
.
18.(本题满分l2分)
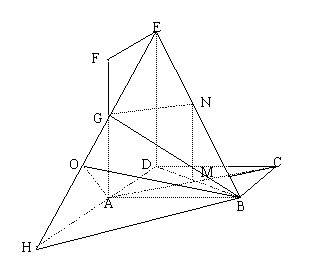
如图所示,正方形ABCD和矩形ADEF所在平面相互垂直,
 G是AF的中点.
G是AF的中点.
(I)求证:AC∥平面GBE;
(Ⅱ)若直线BE与平面ABCD成45o角,
求二面角B―GE―D的大小.
19.(本题满分12分)
从某批产品中,有放回地抽取产品2次,每次随机抽取1件,假设事件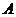 :“取出的2件产品中至多有一件是二等品”的概率
:“取出的2件产品中至多有一件是二等品”的概率
(I)求从该批产品中任取1件是二等品的概率P
(II)若该批产品共100件,从中一次性任意抽取2件,用 表示取出的2件产品中的二等品的件数,求
表示取出的2件产品中的二等品的件数,求 的分布列及期望。
的分布列及期望。
20.(本题满分12分)
已知三次函数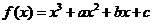 在
在 ,(
,( )上单调递增,在(-1,2)上单调递减,当且仅当
)上单调递增,在(-1,2)上单调递减,当且仅当
(I)求函数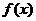 的解析式;
的解析式;
(II)若函数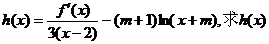 的单调区间和极值。
的单调区间和极值。
21.(本题满分14分)
已知椭圆 C: 的一条准线方程为
的一条准线方程为
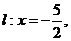 且左焦点F到的
且左焦点F到的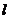 距离为
距离为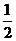 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F的直线交椭圆C于两点A、B、交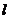 于点M,若
于点M,若 ,
证明
,
证明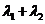 为定值。
为定值。
22.(本题满分12分)
已知数列 满足
满足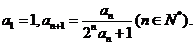
(Ⅰ)求数列 的通项
的通项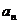 ;
;
(Ⅱ)设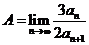 ,证明:对任意m≥2,且
,证明:对任意m≥2,且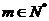 ,都有
,都有 。
。
渭南市崇宁中学3月月考试卷
高三数学(理科)
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
B
B
C
C
B
C
C
A
B
A
C
题号
13
14
15
16
答案
[1/3,2)
-2
1
3899
(1)(2)(3)(4)
三、解答题:(作答时标清题号)
17.解:(1)∵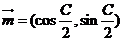 ,
,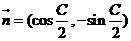 ,
,
∴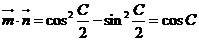 .
…………2分
.
…………2分
又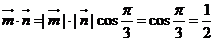 , …………4分
, …………4分
∴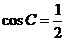 ,∴
,∴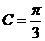 .
…………6分
.
…………6分
(2)∵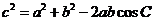 ,
, ,
,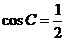 ,
,
∴ . …………8分
. …………8分
 ∵
∵ ,
,
∴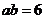 .
.
∴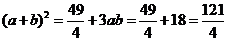 ,
,
∴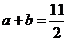 .…………10分
.…………10分
18.(1)证明:连结BD交AC于点M,取BE的中点N,
连结MN,则MN∥ED且MN=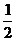 ED,依题意,
ED,依题意,
知AG∥ED且AG=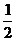 ED,
ED,
∴MN∥AG且MN=AG.
故四边形MNAG是平行四边形, AM∥GN,
即AC∥GN,…………3分
又∵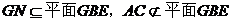
∴ AC∥平面GBE.…………6分
(2)解:延长EG交DA的延长线于H点,
连结BH,作AO⊥GH于O点,连结BO.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,AB⊥AD
∴ AB⊥平面ADEF,由三垂线定理,知AB⊥GH,
故∠AOB就是二面角B-GE-D的平面角.…………8分
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD
∴ ED⊥平面ABCD,
故∠EBD就是直线BE与平面ABCD成的角,……10分
知∠EBD=45°,设AB=a,则BE=BD=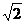 a.
a.
在直角三角形AGH中:AH=AD= a,AG=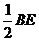 =
= a,
a,
HG=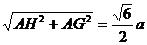 ,AO=
,AO=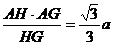 .
.
在直角三角形ABO中:tan∠AOB= .
.
∴ ∠AOB=60°.故二面角B-GE-D的大小为60°.…………12分
19.解:(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件是二等品”.则A0.A1互斥,且A=A0+A1.
故P (A)=P (A0+A1)=P (A0)+P (A1)=(1-p)2+C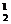 p (1-p)=1-p2.
p (1-p)=1-p2.
依题意,知1-p2=0.96,又p>0,得p=0.2.…………6分
(2)(理)ξ可能的取值为0,1,2.
若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件,故
P(ξ=0)=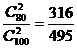 .P(ξ=1)=
.P(ξ=1)=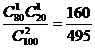 .
.
P(ξ=2)= .…………9分
.…………9分
所以ξ的分布列为
ξ
0
1
2
P

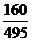

 ξ的期望
ξ的期望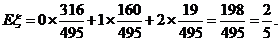 …………12分
…………12分
20.解 (1) 在
在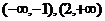 上单调递增,
上单调递增,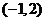 上单调递减,
上单调递减,
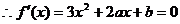 有两根
有两根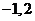 ,
,
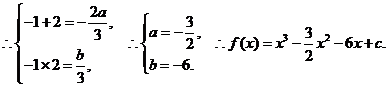 ……4分
……4分
令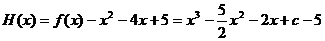 ,
,
则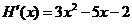 ,
,
因为 在
在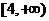 上恒大于0,所以
上恒大于0,所以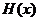 在
在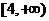 上单调递增,
上单调递增,
故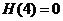 ,
,  ,
,
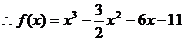 . ……………6分
. ……………6分
(2)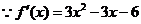 ,
,
 .
.
 .
………………8分
.
………………8分
①当 时,
时,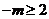 ,定义域为
,定义域为 ,
,
 恒成立,
恒成立,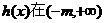 上单调递增;
…………9分
上单调递增;
…………9分
②当 时,
时,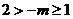 ,定义域:
,定义域: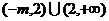 ,
,
 恒成立,
恒成立,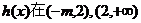 上单调递增; …………10分
上单调递增; …………10分
③当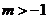 时,
时, ,定义域:
,定义域: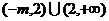 ,
,
由 得
得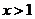 ,由
,由 得
得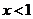 .
.
故在 上单调递增;在
上单调递增;在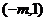 上单调递减. …………11分
上单调递减. …………11分
所以当 时,
时,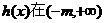 上单调递增,故
上单调递增,故 无极值;
无极值;
当 时,
时,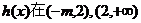 上单增;故
上单增;故 无极值.
无极值.
当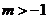 时,
时, 在
在 上单调递增;在
上单调递增;在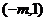 上单调递减.
上单调递减.
故 有极小值,且
有极小值,且 的极小值为
的极小值为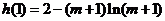 . …12分
. …12分
21. (本题12分)
解:(Ⅰ)依题意得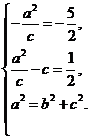 …………2分
…………2分
解方程组得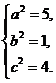
 .
………4分
.
………4分
(Ⅱ)依题意可知直线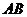 的斜率存在,
的斜率存在,
当斜率为0时,直线 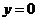 和椭圆交于
和椭圆交于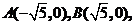
和直线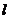 交于
交于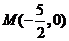 点,则易知
点,则易知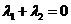 .
.
当斜率不为0时,
可设直线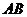 方程为
方程为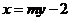 (
(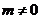 ),
),
 .
.
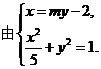
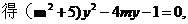 ………6分
………6分

 .
………8分
.
………8分
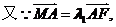
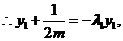 则
则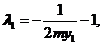
同理 ,
……10分
,
……10分
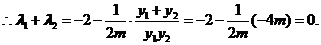
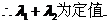 ………11分
………11分
综上所述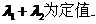 ………12分
………12分
22.解(Ⅰ)由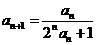 得
得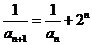 ,
……2分
,
……2分

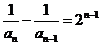 ,
,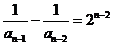

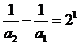 ,
,
以上各式相加得:  ,
,
 ,即
,即 (
(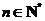 ). …………………………5分
). …………………………5分
(Ⅱ)
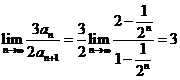 , ……………………6分
, ……………………6分
当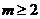 且
且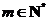 时,
时,

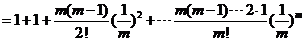 ……………………8分
……………………8分
 …10分
…10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com