|
试题详情
所以异面直线AE和PB所成角的大小为 ………………8分
(2)因为E是PC中点,所以E到平面ABC的距 试题详情
离为 …………10分 …………10分 试题详情
 …………12分 …………12分 试题详情
试题详情
为圆 的直径. 的直径. 试题详情
(1)求证: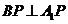 ; ; 试题详情
试题详情
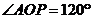 ,求异面直线 ,求异面直线 与 与 所成的角(用 所成的角(用
反三角函数值表示结果). 试题详情
试题详情
试题详情
由题意 ,解得 ,解得 . (6分) . (6分) 试题详情
试题详情
试题详情
试题详情
试题详情
3、(2009上海奉贤区模拟考)在直三棱柱ABC-A1B1C1中,∠ABC=90°, AB=BC=1. (1)求异面直线B1C1与AC所成角的大小; (2)若直线A1C与平面ABC所成角为45°, 求三棱锥A1-ABC的体积. 试题详情
试题详情
∠ABC=90°, AB=BC=1,所以 , -------(2分) , -------(2分) 试题详情
试题详情
试题详情
试题详情
所以 -------(2分) -------(2分) 试题详情
4、(2009冠龙高级中学3月月考)在棱长为2的正方体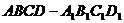 中,(如图) 中,(如图) 试题详情
试题详情
(1)
求三棱锥 的体积; 的体积; 试题详情
求 与底面 与底面 所成的角的大小.(结果用反三角函数表示) 所成的角的大小.(结果用反三角函数表示) 试题详情
(1) . . 试题详情
试题详情
试题详情
 5、(2009闵行三中模拟) 5、(2009闵行三中模拟)
试题详情
5.(本题满分12分)如图,在棱长为2的正方体 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示). 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示). 解】过E作EF⊥BC,交BC于F,连接DF. ∵ EF⊥平面ABCD, 试题详情
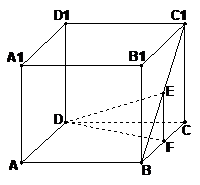 ∴ ∠EDF是直线DE与平面ABCD所成的角. ……………4分 ∴ ∠EDF是直线DE与平面ABCD所成的角. ……………4分
试题详情
由题意,得EF=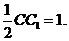 试题详情
∵ 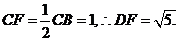 …………………………..8分 …………………………..8分 试题详情
∵ EF⊥DF, ∴  ……………..10分 ……………..10分 试题详情
故直线DE与平面ABCD所成角的大小是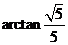 ….12分 ….12分 试题详情
试题详情
试题详情
试题详情
故 ,且 ,且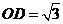 . . 试题详情
又 , , 试题详情
所以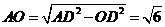 . . 试题详情
而圆锥体的底面圆面积为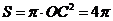 , , 试题详情
所以圆锥体体积 . . 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(2)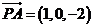 ,可设 ,可设 , , 试题详情
所以向量 的坐标为 的坐标为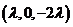 ,
…… 8分 ,
…… 8分 试题详情
平面 的法向量为 的法向量为 . . 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(1)求证: ; ; 试题详情
(2)求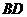 与平面 与平面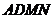 所成的角; 所成的角; 解: 试题详情
试题详情
所以 。 。
试题详情
试题详情
又 ,即 ,即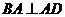 , , 试题详情
试题详情
试题详情
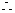  。
………… 5分 。
………… 5分
试题详情
(2)连结 , , 试题详情
试题详情
试题详情
在 中, 中, , , 试题详情
试题详情
在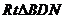 中, 中,  , , 试题详情
又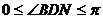 , , 试题详情
故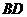 与平面 与平面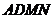 所成的角是 所成的角是 。 …… 12分 。 …… 12分 备注:(1)、(2)也可以用向量法: 试题详情
(1)以 点为坐标原点建立空间直角坐标系 点为坐标原点建立空间直角坐标系 ,如图所示(图略) ,如图所示(图略) 试题详情
试题详情
因为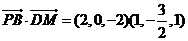 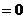 , , 试题详情
所以 。
…… 5分 。
…… 5分 试题详情
(2)因为 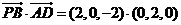 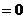 试题详情
所以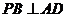 ,又 ,又 , , 试题详情
试题详情
试题详情
则 , , 试题详情
试题详情
试题详情
试题详情
 (Ⅰ)求四棱锥 (Ⅰ)求四棱锥 的体积; 的体积;
(Ⅱ)求异面直线OB与MD所成角的大小. 试题详情
解:(Ⅰ)由已知可求得,正方形 的面积 的面积 ,……………………………2分 ,……………………………2分 试题详情
所以,求棱锥 的体积 的体积 ………………………………………4分 ………………………………………4分 (Ⅱ)方法一(综合法) 试题详情
试题详情
则 为异面直线OC与 为异面直线OC与 所成的角(或其补角) ………………………………..1分 所成的角(或其补角) ………………………………..1分 试题详情
由已知,可得 , , 试题详情
试题详情
 为直角三角形 ……………………………………………………………….2分 为直角三角形 ……………………………………………………………….2分
试题详情
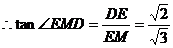 , ……………………………………………………………….4分 , ……………………………………………………………….4分
试题详情
 . .
试题详情
所以,异面直线OC与MD所成角的大小 . …………………………..1分 . …………………………..1分 方法二(向量法) 试题详情
以AB,AD,AO所在直线为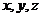 轴建立坐标系, 轴建立坐标系, 试题详情
则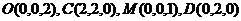 ,
……………………………………………………2分 ,
……………………………………………………2分 试题详情
 , ,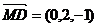 ,
………………………………………………………………………………..2分 ,
………………………………………………………………………………..2分
试题详情
设异面直线OC与MD所成角为 , , 试题详情
 .……………………………….. …………………………3分 .……………………………….. …………………………3分
试题详情
 OC与MD所成角的大小为 OC与MD所成角的大小为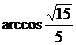 .……………………………………………1分 .……………………………………………1分 试题详情
| 
 立体几何
立体几何 cm2,已知
cm2,已知
 到过球面上A、B、C三点的截面的距离等于此球半径的一半,若
到过球面上A、B、C三点的截面的距离等于此球半径的一半,若 ,则球的体积为________________。
,则球的体积为________________。
 3、(2009上海十校联考)如图,设
3、(2009上海十校联考)如图,设 是棱长为
是棱长为 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有 个顶点;②有
个顶点;②有 条棱;③有
条棱;③有 个面;④表面积为
个面;④表面积为 ;⑤体积为
;⑤体积为 .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)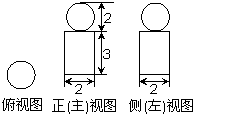 4、(2009上海闸北区)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是………………………………………( )
4、(2009上海闸北区)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是………………………………………( ) B.
B.
 D.
D.