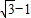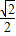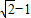科目:gzsx
来源:
题型:
设椭圆
+=1(a>b>0)的左、右焦点分别为F
1,F
2,A是椭圆上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为
|OF1|.
(I)证明:
a=b;
(II)设Q
1,Q
2为椭圆上的两个动点,OQ
1⊥OQ
2,过原点O作直线Q
1Q
2的垂线OD,垂足为D,求点D的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
设双曲线
-=1(a>0,b>0)的左、右焦点分别为F
1、F
2,A是双曲线渐近线上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为
|OF1|,则渐近线的斜率为( )
查看答案和解析>>
科目:gzsx
来源:2007年天津市高考数学试卷(理科)(解析版)
题型:解答题
设椭圆

=1(a>b>0)的左、右焦点分别为F
1,F
2,A是椭圆上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为

.
(I)证明:
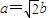
;
(II)设Q
1,Q
2为椭圆上的两个动点,OQ
1⊥OQ
2,过原点O作直线Q
1Q
2的垂线OD,垂足为D,求点D的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
(08年临沂市质检一理) (12分)设椭圆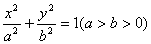 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 ;
;
(1)求椭圆的离心率;
(2)若左焦点F1(-1,0)设过点F1且不与坐标轴垂直的直线交椭圆于B,C两点,线段BC的垂直平分线与x轴交于G,求点G横坐标的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012年云南省昆明市高三复习教学质量检测数学试卷(理科)(解析版)
题型:选择题
设双曲线
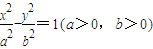
的左、右焦点分别为F
1、F
2,A是双曲线渐近线上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为
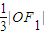
,则渐近线的斜率为( )
A.
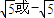
B.
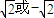
C.1或-1
D.
查看答案和解析>>
科目:gzsx
来源:天津高考真题
题型:解答题
设椭圆

的左、右焦点分别为F
1,F
2,A是椭圆上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为
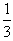
|OF
1|,
(Ⅰ)证明a=

b;
(Ⅱ)求t∈(0,b)使得下述命题成立:设圆x
2+y
2=t
2上任意点M(x
0,y
0)处的切线交椭圆于Q
1,Q
2两点,则OQ
1⊥OQ
2。
查看答案和解析>>
科目:gzsx
来源:2007年普通高等学校招生全国统一考试、理科数学(天津卷)
题型:044
设椭圆 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
.
(Ⅰ)证明 ;
;
(Ⅱ)设Q1,Q2为椭圆上的两个动点,OQ1⊥OQ2,过原点O作直线Q1Q2的垂线OD,垂足为D,求点D的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:2007年普通高等学校招生全国统一考试 文科数学(天津卷)
题型:044
设椭圆 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
.
(Ⅰ)证明a= ;
;
(Ⅱ)求t∈(0,b)使得下述命题成立:设圆x2+y2=t2上任意点M(x0,y0)处的切线交椭圆于Q1,Q2两点,则OQ1⊥OQ2.
查看答案和解析>>
科目:gzsx
来源:2012年云南省昆明市高三复习教学质量检测数学试卷(文科)(解析版)
题型:选择题
设双曲线

的左、右焦点分别为F
1、F
2,A是双曲线渐近线上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为
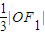
,则渐近线的斜率为( )
A.

B.

C.1或-1
D.

查看答案和解析>>
科目:gzsx
来源:天津高考真题
题型:解答题
设椭圆

的左、右焦点分别为F
1,F
2,A是椭圆上的一点,AF
2⊥F
1F
2,原点O到直线AF
1的距离为
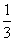
|OF
1|,
(Ⅰ)证明:a=

b;
(Ⅱ)设Q
1,Q
2为椭圆上的两个动点,OQ
1⊥OQ
2,过原点O作直线Q
1Q
2的垂线OD,垂足为D,求点D的轨迹方程。
查看答案和解析>>
科目:gzsx
来源:
题型:单选题
设双曲线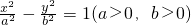 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为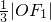 ,则渐近线的斜率为
,则渐近线的斜率为
- A.
- B.
- C.
1或-1
- D.
查看答案和解析>>
科目:gzsx
来源:
题型:
设椭圆
C:+=1(a>0)的左、右焦点分别为F
1、F
2,A是椭圆C上的一点,且
•=0,坐标原点O到直线AF
1的距离为
|OF1|.
(I)求椭圆C的方程;
(II)设Q是椭圆C上的一点,过Q的直线l交x轴于点P(-1,0),较y轴于点M,若
=2,求直线l的方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2011•宝坻区一模)设椭圆C:
+=1(a>0)的左右焦点分别为F
1、F
2,A是椭圆C上的一点,
•=0,坐标原点O到直线AF
1的距离为
|OF
1|.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|
|=2|
|,求直线l的斜率.
查看答案和解析>>
科目:gzsx
来源:
题型:
设椭圆
C:+=1(a>0)的左右焦点分别为F
1、F
2,A是椭圆C上的一点,且
•=0,坐标原点O到直线AF
1的距离为
|OF1|.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|MQ|=2|QF|,求直线l的斜率.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
设椭圆
C:+=1(a>0)的左、右焦点分别为F
1、F
2,A是椭圆C上的一点,且
•=0,坐标原点O到直线AF
1的距离为
|OF1|.
(I)求椭圆C的方程;
(II)设Q是椭圆C上的一点,过Q的直线l交x轴于点P(-1,0),较y轴于点M,若
=2,求直线l的方程.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
设椭圆C:
+=1(a>0)的左右焦点分别为F
1、F
2,A是椭圆C上的一点,
•=0,坐标原点O到直线AF
1的距离为
|OF
1|.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|
|=2|
|,求直线l的斜率.
查看答案和解析>>
科目:gzsx
来源:普宁市模拟
题型:解答题
设椭圆
C:+=1(a>0)的左右焦点分别为F
1、F
2A是椭圆C上的一点,且
.=0,坐标原点O到直线AF
1的距离为
|OF1|.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|MQ|=2|QF|,求直线l的斜率.
查看答案和解析>>
科目:gzsx
来源:
题型:
设椭圆
+=1(a>b>0)的左、右焦点分别为F
1、F
2,A是椭圆上的一点,AF
2⊥AF
1,原点O到直线AF
1的距离为
|OF1|,则椭圆的离心率为( )
查看答案和解析>>
科目:gzsx
来源:2011-2012学年海南省琼海市嘉积中学高三(上)质量检测数学试卷3(理科)(解析版)
题型:选择题
设椭圆
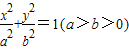
的左、右焦点分别为F
1、F
2,A是椭圆上的一点,AF
2⊥AF
1,原点O到直线AF
1的距离为
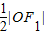
,则椭圆的离心率为( )
A.

B.
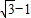
C.
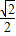
D.
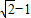
查看答案和解析>>
科目:gzsx
来源:
题型:单选题
设椭圆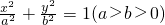 的左、右焦点分别为F1、F2,A是椭圆上的一点,AF2⊥AF1,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是椭圆上的一点,AF2⊥AF1,原点O到直线AF1的距离为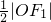 ,则椭圆的离心率为
,则椭圆的离心率为
- A.
- B.
- C.
- D.
查看答案和解析>>

 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
.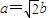 ;
;![]() 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为![]() ;
;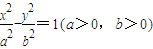 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为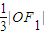 ,则渐近线的斜率为( )
,则渐近线的斜率为( )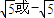
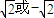
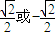
 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为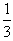 |OF1|,
|OF1|, b;
b;![]() 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为![]() .
.![]() ;
;![]() 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为![]() .
.![]() ;
; 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为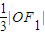 ,则渐近线的斜率为( )
,则渐近线的斜率为( )


 的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为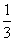 |OF1|,
|OF1|, b;
b;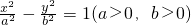 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为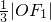 ,则渐近线的斜率为
,则渐近线的斜率为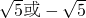
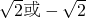
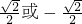
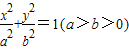 的左、右焦点分别为F1、F2,A是椭圆上的一点,AF2⊥AF1,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是椭圆上的一点,AF2⊥AF1,原点O到直线AF1的距离为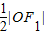 ,则椭圆的离心率为( )
,则椭圆的离心率为( )