精英家教网 >
试题搜索列表 >已知函数,. (1)求函数的最小正周期及对称中心 (2)求函数的减区间及对称轴
已知函数,. (1)求函数的最小正周期及对称中心 (2)求函数的减区间及对称轴答案解析
科目:gzsx
来源:
题型:
已知函数
f(x)=sin4x-cos4x+2sinxcosx+1(1)求该函数的最小正周期及对称中心;
(2)求该函数在[0,π]上的单调增区间.
查看答案和解析>>
科目:gzsx
来源:2015届河南省郑州市高一下学期期中考试数学试卷(解析版)
题型:解答题
已知 ,
, .
.
(1)求函数 的最小正周期及对称中心;
的最小正周期及对称中心;
(2)求函数的单调递减区间.
查看答案和解析>>
科目:gzsx
来源:江苏省期末题
题型:解答题
已知函数
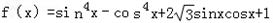
(1)求该函数的最小正周期及对称中心;
(2)求该函数在[0,π]上的单调增区间.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数
f(x)=-2sin2x+2sinxcosx+1.
(1)求f(x)的最小正周期及对称中心;
(2)若
x∈[-,],求f(x)的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知向量
=(2sinx,cosx),
=(
cosx,2cosx),定义函数f(x)=
•
-1.
(1)求函数f(x)的最小正周期及对称中心;
(2)当x∈[-
,
]时,求函数f(x)的单调增区间.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=(sin2x+cos2x)
2+3-2sin
22x.
(1)求f(x)的最小正周期及对称中心;
(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移
个单位长度得到的,当
x∈[0,]时,求y=g(x)的值域.
查看答案和解析>>
科目:gzsx
来源:2010年高考数学调研试卷(解析版)
题型:解答题
已知函数

.
(1)求f(x)的最小正周期及对称中心;
(2)若

,求f(x)的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:2011年江苏省连云港市赣榆高级中学高三3月调研数学试卷(解析版)
题型:解答题
已知函数

.
(1)求f(x)的最小正周期及对称中心;
(2)若

,求f(x)的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:2010年江苏省高一下学期期末考试数学卷
题型:解答题
(本题满分12分)
已知函数 ,求
,求
(1) 求 的最小正周期及对称中心;
的最小正周期及对称中心;
(2) 当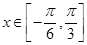 时,求
时,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省荆州中学高三第二次质量检测数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)=(sin2x+cos2x)
2+3-2sin
22x.
(1)求f(x)的最小正周期及对称中心;
(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移
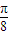
个单位长度得到的,当
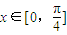
时,求y=g(x)的值域.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知向量
=(2sinx,cosx),
=(
cosx,2cosx),定义函数f(x)=
•
-1.
(1)求函数f(x)的最小正周期及对称中心;
(2)当x∈[-
,
]时,求函数f(x)的单调增区间.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年重庆第二外国语学校高三(下)3月月考数学试卷(文科)(解析版)
题型:解答题
已知向量

=(2sinx,cosx),

=(
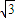
cosx,2cosx),定义函数f(x)=
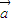
•
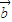
-1.
(1)求函数f(x)的最小正周期及对称中心;
(2)当x∈[-

,
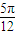
]时,求函数f(x)的单调增区间.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知函数
f(x)=-2sin2x+2sinxcosx+1.
(1)求f(x)的最小正周期及对称中心;
(2)若
x∈[-,],求f(x)的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知函数f(x)=(sin2x+cos2x)2+3-2sin22x.
(1)求f(x)的最小正周期及对称中心;
(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移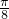 个单位长度得到的,当
个单位长度得到的,当 时,求y=g(x)的值域.
时,求y=g(x)的值域.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数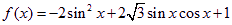
⑴求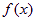 的最小正周期及对称中心;ks5u
的最小正周期及对称中心;ks5u
⑵若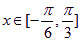 ,求
,求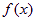 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年四川省高三3月月考数学试卷(解析版)
题型:解答题
查看答案和解析>>
科目:gzsx
来源:
题型:
(本题满分12分)
已知函数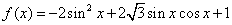 ,求
,求
求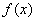 的最小正周期及对称中心;
的最小正周期及对称中心;
当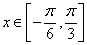 时,求
时,求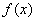 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
(本题满分14分)
已知函数
⑴求 的最小正周期及对称中心;
的最小正周期及对称中心;
⑵若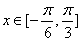 ,求
,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
(本题满分12分)
已知函数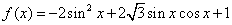 ,求
,求
求 的最小正周期及对称中心;
的最小正周期及对称中心;
当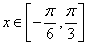 时,求
时,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>

 .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值. ,求
,求 的最小正周期及对称中心;
的最小正周期及对称中心;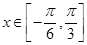 时,求
时,求 的最大值和最小值.
的最大值和最小值.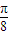 个单位长度得到的,当
个单位长度得到的,当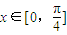 时,求y=g(x)的值域.
时,求y=g(x)的值域. =(2sinx,cosx),
=(2sinx,cosx), =(
=(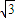 cosx,2cosx),定义函数f(x)=
cosx,2cosx),定义函数f(x)=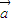 •
•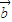 -1.
-1. ,
,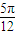 ]时,求函数f(x)的单调增区间.
]时,求函数f(x)的单调增区间. =(2sinx,cosx),
=(2sinx,cosx), =(
=( cosx,2cosx),定义函数f(x)=
cosx,2cosx),定义函数f(x)= •
• -1.
-1.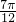 ,
,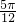 ]时,求函数f(x)的单调增区间.
]时,求函数f(x)的单调增区间.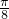 个单位长度得到的,当
个单位长度得到的,当 时,求y=g(x)的值域.
时,求y=g(x)的值域. 的图像过点
的图像过点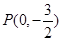
 的最小正周期以及对称中心坐标;
的最小正周期以及对称中心坐标; 内角
内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,且
,且 ,
, 的形状,并说明理由。
的形状,并说明理由。