
科目:gzsx 来源: 题型:
科目:gzsx 来源:高考数学一轮复习必备(第73课时):第九章 直线、平面、简单几何体-直线和平面平行及平面与平面平行(解析版) 题型:解答题
科目:gzsx 来源:2011年高三数学精品复习18:线面关系(解析版) 题型:解答题
科目:gzsx 来源: 题型:
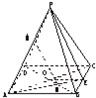 已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.
已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.科目:gzsx 来源: 题型:
 已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为
已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为| 2 |
科目:gzsx 来源: 题型:
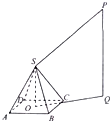 房屋的天花板上点P处有一光源,P在地面上的射影为Q,在地面上放置正棱锥S-ABCD,底面ABCD接触地面,已知正四棱锥S-ABCD的高为1米,底面ABCD的边长为
房屋的天花板上点P处有一光源,P在地面上的射影为Q,在地面上放置正棱锥S-ABCD,底面ABCD接触地面,已知正四棱锥S-ABCD的高为1米,底面ABCD的边长为| 1 | 2 |
科目:gzsx 来源:2013年全国普通高等学校招生统一考试文科数学(全国大纲卷解析版) 题型:选择题
已知正四棱锥 中,
中, ,则CD与平面
,则CD与平面 所成角的正弦值等于( )
所成角的正弦值等于( )
A. B.
B. C.
C. D.
D.
科目:gzsx 来源:2012届浙江省高三调研测试文科数学试卷 题型:解答题
(本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为 .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.

科目:gzsx 来源:2011-2012学年浙江省招生适应性考试文科数学试卷(解析版) 题型:解答题
(本题满分14分)已知正四棱锥 的底面边长为
的底面边长为 ,
, 为
为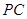 中点.
中点.
(Ⅰ)求证: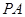 //平面
//平面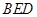 ;
;
(Ⅱ)若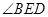 是二面角
是二面角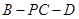 的平面角,求直线
的平面角,求直线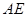 与平面
与平面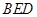 所成角的余弦值.
所成角的余弦值.
科目:gzsx 来源:2011-2012学年浙江省高三第二学期第一次统考文科数学 题型:解答题
(本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为 .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.

科目:gzsx 来源:导学大课堂选修数学2-1苏教版 苏教版 题型:044
已知正四棱锥S-ABCD的底边长为4,高为6,P是高SO的中点,Q是侧面SBC的重心,求
(1)P、Q两点间的距离;
(2)异面直线PQ与BS所成的角;
(3)直线PQ与底面ABCD所成的角.
科目:gzsx 来源:数学教研室 题型:044
已知正四棱锥S-ABCD的棱长均为13,E、F分别是SA、BD上的点,且SE∶EA=BF∶FD=5∶8.
(1)求证:直线EF∥平面SBC;
(2)求四棱锥S-ABCD的体积.
科目:gzsx 来源:2012-2013学年浙江省重点中学高二(上)期中数学试卷(理科)(解析版) 题型:解答题
 .M为线段PC的中点.
.M为线段PC的中点.
科目:gzsx 来源: 题型:044
已知正四棱锥P—ABCD的底面边长和各侧棱长都是13,M、N分别是PA、BD上的点,且PM∶MA=BN∶ND=5∶8.
(1)求证:MN∥平面PBC;
(2)求直线MN与平面ABCD所成角的正弦值.
科目:gzsx 来源: 题型:044
已知正四棱锥
S-ABCD的棱长均为13,E、F分别是SA、BD上的点,且SE∶EA=BF∶FD=5∶8.(1)
求证:直线EF∥平面SBC;(2)
求四棱锥S-ABCD的体积.科目:gzsx 来源: 题型:022
科目:gzsx 来源:浙江省2012届高三调研考试数学文科试题 题型:044
已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为![]() .M为线段PC的中点.
.M为线段PC的中点.
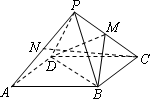
(Ⅰ)求证:PA∥平面MDB;
(Ⅱ)N为AP的中点,求CN与平面MBD所成角的正切值.
科目:gzsx 来源:2013年普通高等学校招生全国统一考试大纲卷理数 题型:013
已知正四棱锥ABCD-A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于
A.![]()
B.![]()
C.![]()
D.![]()
科目:gzsx 来源:数学教研室 题型:044
(1)求证:MN∥平面PBC;
(2)求直线MN与平面ABCD所成角的正弦值.
科目:gzsx 来源: 题型:
已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为![]() .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
 |