
科目:gzsx 来源:2013-2014学年山东省潍坊市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
已知正四棱柱 的外接球直径为
的外接球直径为 ,底面边长
,底面边长 ,则侧棱
,则侧棱 与平面
与平面 所成角的正切值为_________。
所成角的正切值为_________。
科目:gzsx 来源:2012-2013学年湖北省八校高三第二次联考文科数学试卷(解析版) 题型:选择题
已知两个正数 ,
,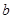 的等差中项是
的等差中项是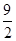 ,一个等比中项是
,一个等比中项是 ,且
,且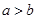 ,则抛物线
,则抛物线 的焦点坐标为( )
的焦点坐标为( )
A. B.
B.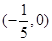 C.
C. D.
D.
科目:gzsx 来源:数学教研室 题型:044
已知点P在平面ABC外,△ABC是等腰直角三角形,∠ABC=90°,△PAB是正三角形,PA⊥BC
(1)求证:平面PAB⊥平面ABC;
(2)求二面角P-AC-B正切值的大小.
科目:gzsx 来源:2011年河北省唐山一中高考数学仿真试卷4(文科)(解析版) 题型:选择题
 ,BD=1,在外接球面上两点A、B间的球面距离是( )
,BD=1,在外接球面上两点A、B间的球面距离是( )



科目:gzsx 来源: 题型:044
已知点
P在平面ABC外,△ABC是等腰直角三角形,∠ABC=90°,△PAB是正三角形,PA⊥BC(1)
求证:平面PAB⊥平面ABC;(2)
求二面角P-AC-B正切值的大小.科目:gzsx 来源:广东省高考数学一轮复习:10.3 球及其表面积和体积(解析版) 题型:解答题

科目:gzsx 来源:2009年上海市静安、杨浦、青浦、宝山区高考数学二模试卷(文理合卷)(解析版) 题型:解答题

科目:gzsx 来源: 题型:
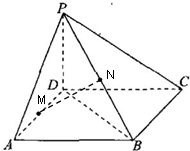 已知四棱锥P-ABCD的底面ABCD是正方形,M,N分别为AD,PB的中点,且PD⊥底面ABCD,其中PD=AD=a.
已知四棱锥P-ABCD的底面ABCD是正方形,M,N分别为AD,PB的中点,且PD⊥底面ABCD,其中PD=AD=a.科目:gzsx 来源: 题型:
 已知四棱锥P-ABCD的底面ABCD是边长为4的正方形,PD⊥平面ABCD,PD=6,E,F分别为PB,AB中点.
已知四棱锥P-ABCD的底面ABCD是边长为4的正方形,PD⊥平面ABCD,PD=6,E,F分别为PB,AB中点.科目:gzsx 来源: 题型:
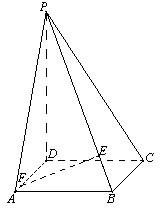 如图,已知四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=2.
如图,已知四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=2.| PE |
| EB |
| DF |
| FA |
| 1 |
| 4 |
科目:gzsx 来源: 题型:
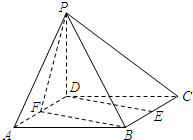 如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
| ||
| 6 |
科目:gzsx 来源: 题型:
 如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,点F为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,点F为PC的中点.科目:gzsx 来源: 题型:
 已知四棱锥P-ABCD的底面ABCD是正方形,且PD⊥底面ABCD,其中PD=AD=a.
已知四棱锥P-ABCD的底面ABCD是正方形,且PD⊥底面ABCD,其中PD=AD=a.科目:gzsx 来源: 题型:
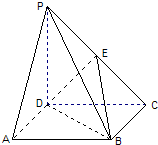 如图,已知四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.科目:gzsx 来源: 题型:
 (2012•安徽模拟)如图,已知四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,∠BAD=90°,PB=PC=CD=2AB=4,AC=2
(2012•安徽模拟)如图,已知四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,∠BAD=90°,PB=PC=CD=2AB=4,AC=2| 7 |
科目:gzsx 来源: 题型:
| SA | AB |