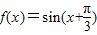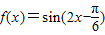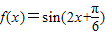科目:gzsx 来源: 题型:
| a |
| b |
| 3 |
| 2 |
| a |
| 3 |
| b |
| π |
| 12 |
| π |
| 4 |
科目:gzsx 来源: 题型:
| a |
| 3 |
| b |
| π |
| 2 |
| a |
| b |
| 3 |
| 2 |
| π |
| 12 |
| π |
| 4 |
科目:gzsx 来源:山东省莱州一中2012届高三第二次质量检测数学文科试题 题型:044
若向量 ,其中
,其中 ,设函数
,设函数 ,其周期为π,且x=
,其周期为π,且x= 是它的一条对称轴.
是它的一条对称轴.
(1)求f(x)的解析式;
(2)当 时,不等式f(x)+a>0恒成立,求实数a的取值范围.
时,不等式f(x)+a>0恒成立,求实数a的取值范围.
科目:gzsx 来源:荆门市2008届高三数学试题(理)模拟训练题 题型:013
已知定义在R上的奇函数y=f(x)满足![]() 为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是
为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是
(1)y=f(x)是周期函数
(2)x=π是它的一条对称轴
(3)(-π,0)是它图象的一个对称中心
(4)当![]() 时,它一定取最大值
时,它一定取最大值
A.(2)(4)
B.(2)(3)
C.(1)(2)
D.(1)(3)
科目:gzsx 来源:江苏常州一中2007-2008学年度高三第一学期第一阶段考试试题数学 题型:013
已知定义在R上的奇函数![]() 为偶函数,对于函数y=f(x)有下列几种描述,
为偶函数,对于函数y=f(x)有下列几种描述,
(1)y=f(x)是周期函数
(2)x=π是它的一条对称轴
(3)(-π,0)是它图象的一个对称中心
(4)当![]() 时,它一定取最大值
时,它一定取最大值
其中描述正确的是
A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(2)(3)
科目:gzsx 来源: 题型:
| 1 |
| 5 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| A、①②⑤ | B、②⑤ |
| C、②③④ | D、①③⑤ |
科目:gzsx 来源: 题型:
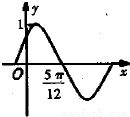
 设函数f(x)=sin(ωx+φ)(ω>0,0<φ<
设函数f(x)=sin(ωx+φ)(ω>0,0<φ<| π |
| 2 |
| π |
| 6 |
A、f(x)=sin(x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(4x+
| ||
D、f(x)=sin(2x+
|
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
(1)求椭圆的方程;
(2)设A1、A2分别是椭圆的左顶点和右顶点,P是椭圆上满足|PA1|-|PA2|=2的一点,求tan∠A1PA2的值;
(3)若过点(1,0)的直线与以原点为顶点、A2为焦点的抛物线相交于点M、N,求MN中点Q的轨迹方程.
科目:gzsx 来源:2006年高考第一轮复习数学:8.5 轨迹问题(解析版) 题型:解答题
科目:gzsx 来源:不详 题型:解答题
科目:gzsx 来源:2011年四川省宜宾市南溪一中高考数学一诊模拟试卷3(文科)(解析版) 题型:解答题
 ,其中
,其中 ,设函数
,设函数 ,其周期为π,且
,其周期为π,且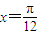 是它的一条对称轴.
是它的一条对称轴.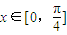 时,不等式f(x)+a>0恒成立,求实数a的取值范围.
时,不等式f(x)+a>0恒成立,求实数a的取值范围.科目:gzsx 来源:导学大课堂必修二数学苏教版 苏教版 题型:044
已知两圆C1:x2+y2-6y=0,C2:(x-23)2+(y-1)2=1.
(1)求证两圆外切,且x轴是它们的一条外公切线;
(2)求出它的另一条外公切线方程.
科目:gzsx 来源:黑龙江省大庆铁人中学2011-2012学年高二第一次阶段测试数学试题 题型:044
已知两圆
C1:x2+y2-6y=0,C2:x2+y2-4(1)求证:两圆外切,x轴是它们的一条外公切线;
(2)求切点间的两段劣弧与x轴所围成的图形的面积.(扇形面积公式:)
科目:gzsx 来源:甘肃省张掖二中2012届高三9月月考数学理科试题 题型:044
若向量![]() ,其中
,其中![]() ,设函数
,设函数![]() ,其周期为π,且
,其周期为π,且![]() 是它的一条对称轴.
是它的一条对称轴.
(1)求f(x)的最小正周期;
(2)当![]() 时,不等式f(x)+a>0恒成立,求实数a的取值范围.
时,不等式f(x)+a>0恒成立,求实数a的取值范围.
科目:gzsx 来源: 题型:
| π |
| 2 |
| π |
| 2 |
科目:gzsx 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| A、①② | B、①③ | C、②④ | D、②③ |
科目:gzsx 来源:2012届甘肃省高三9月月考理科数学试卷 题型:解答题
(本题满分10分) 若向量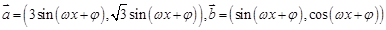 ,其中
,其中 ,设
,设
函数 ,其周期为
,其周期为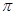 ,且
,且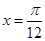 是它的一条对称轴。
是它的一条对称轴。
(1)求 的解析式;
的解析式;
(2)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
科目:gzsx 来源:2011-2012学年山东省高三第二次质量检测文科数学试卷 题型:解答题
若向量 ,其中
,其中 ,设函数
,设函数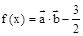 ,其周期为
,其周期为 ,且
,且 是它的一条对称轴。
是它的一条对称轴。
(1)
求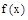 的解析式;
的解析式;
(2)
当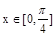 时,不等式
时,不等式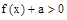 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
科目:gzsx 来源:2010-2011学年福建省福州市高三(上)期末数学试卷(理科)(解析版) 题型:选择题
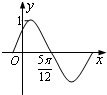
 的部分图象如图所示,直线
的部分图象如图所示,直线 是它的一条对称轴,则函数f(x)的解析式为( )
是它的一条对称轴,则函数f(x)的解析式为( )