精英家教网 >
试题搜索列表 >在抛物线y2=2x和定点A(3,10/3),抛物线上又动点P,P到定点A的距离为d1
在抛物线y2=2x和定点A(3,10/3),抛物线上又动点P,P到定点A的距离为d1答案解析
科目:gzsx
来源:
题型:
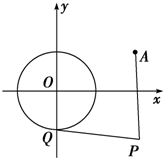
已知圆O:x
2+y
2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图
(1)求a、b间关系;
(2)求|PQ|的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|,
(Ⅰ)求实数a,b间满足的等量关系;
(Ⅱ)求线段PQ长的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:

已知圆O:x
2+y
2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|
(1)求实数a、b间满足的等量关系;
(2)若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.
查看答案和解析>>
科目:gzsx
来源:
题型:

已知圆O:x
2+y
2=1和定点A(2,1),由圆O外一点P向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(Ⅰ)求P点的轨迹方程;
(Ⅱ)求线段PQ长的最小值,并求此时PQ的斜率.
查看答案和解析>>
科目:gzsx
来源:101网校同步练习 高三数学 苏教版(新课标·2004年初审) 苏教版
题型:013
两定点A(―2,―1),B(2,-1)动点P在抛物线y=x2上移动.则△PAB重心G的轨迹方程为
[ ]
A.
B.
C.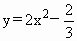
D.
查看答案和解析>>
科目:gzsx
来源:河北省期末题
题型:解答题
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|。
(1)求实数a、b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程。
查看答案和解析>>
科目:gzsx
来源:
题型:
设P(a,b)(b≠0)是平面直角坐标系xOy中的点,l是经过原点与点(1,b)的直线.记Q是直线l与抛物线x
2=2py(p≠0)的异于原点的交点.
(1)已知a=1,b=2,p=2,求点Q的坐标;
(2)已知点P(a,b)(ab≠0)在椭圆 +y2=1上,p=
+y2=1上,p=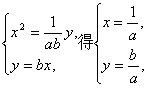 ,求证:点Q落在双曲线4x2-4y2=1上;
,求证:点Q落在双曲线4x2-4y2=1上;
(3)已知动点P(a,b)满足ab≠0,p= ,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由.
,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年陕西省宝鸡中学高一(上)期末数学试卷(解析版)
题型:解答题
已知圆O:x
2+y
2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|
(1)求实数a、b间满足的等量关系;
(2)若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.

查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|,
(Ⅰ)求实数a,b间满足的等量关系;
(Ⅱ)求线段PQ长的最小值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年福建省泉州市南安一中高一(上)期末数学试卷(解析版)
题型:解答题
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|,
(Ⅰ)求实数a,b间满足的等量关系;
(Ⅱ)求线段PQ长的最小值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年四川省成都七中高一(下)期末数学试卷(解析版)
题型:解答题
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是

.
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.
①若M是圆E:(x-2)
2+(y-4)
2=64上任意一点,过M作曲线D的切线,切点是N,求|MN|的取值范围;
②已知F,G是曲线D上不同的两点,对于定点Q(-3,0),有|QF|•|QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.

查看答案和解析>>
科目:gzsx
来源:2011-2012学年湖北省黄冈中学高一(下)期末数学试卷(理科)(解析版)
题型:解答题
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是

.
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.
①若M是圆E:(x-2)
2+(y-4)
2=64上任意一点,过M作曲线D的切线,切点是N,求|MN|的取值范围;
②已知F,G是曲线D上不同的两点,对于定点Q(-3,0),有|QF|•|QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.

查看答案和解析>>
科目:gzsx
来源:
题型:
在△PAB中,已知
A(-,0)、
B(,0),动点P满足|PA|=|PB|+4.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设M(-2,0),N(2,0),过点N作直线l垂直于AB,且l与直线MP交于点Q,试在x轴上确定一点T,使得PN⊥QT;
(Ⅲ)在(Ⅱ)的条件下,设点Q关于x轴的对称点为R,求
•的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
是否存在同时满足下列条件的双曲线?若存在,请求出其方程,若不存在请说明理由.
(1)中心在原点,准线平行于X轴;
(2)离心率
e=;
(3)点A(0,5)到双曲线上的动点P的最小值为2.
查看答案和解析>>
科目:gzsx
来源:新课标高三数学轨迹问题、几何体的结构与三视图专项训练(河北)
题型:填空题
已知两定点A(-2,0)、B(1,0),如果动点P满足|PA|=2|PB|,则点P的轨迹方程为:________
查看答案和解析>>
科目:gzsx
来源:
题型:
已知圆x
2+y
2=25与直线l:y=-

交于A、B,以大于半圆的AB上的动点P为圆心与l相切的圆记为圆P,求△PAB未被圆P覆盖部分的面积的最大值.
查看答案和解析>>
科目:gzsx
来源:2002年高中会考数学必备一本全2002年1月第1版
题型:013
抛物线 最小的抛物线上的动点P(x,y)的坐标是
最小的抛物线上的动点P(x,y)的坐标是
[ ]
A.(1,±1)
B.(0,0)
C.(

,±1)
D.(0,2)
查看答案和解析>>
科目:gzsx
来源:2005-2006学年广东省珠海市高二质量检测数学模拟试卷(理科)(解析版)
题型:解答题
是否存在同时满足下列条件的双曲线?若存在,请求出其方程,若不存在请说明理由.
(1)中心在原点,准线平行于X轴;
(2)离心率

;
(3)点A(0,5)到双曲线上的动点P的最小值为2.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年福建省福州市高二(上)期末数学试卷(期末)(解析版)
题型:选择题
已知点

及抛物线

上的动点P(x,y),则y+|PQ|的最小值是( )
A.2
B.3
C.4
D.

查看答案和解析>>
科目:gzsx
来源:
题型:044
已知
x轴上的一定点A(1,0),Q为椭圆 上的动点,求AQ中点M的轨迹方程.
上的动点,求AQ中点M的轨迹方程.
查看答案和解析>>

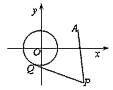
 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA| 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.![]()
![]()
![]()
![]()
![]() +y2=1上,p=
+y2=1上,p=![]() ,求证:点Q落在双曲线4x2-4y2=1上;
,求证:点Q落在双曲线4x2-4y2=1上;![]() ,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由.
,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由.
 .
.
 .
.
 最小的抛物线上的动点P(x,y)的坐标是
最小的抛物线上的动点P(x,y)的坐标是 ,±1)
,±1) ;
; 及抛物线
及抛物线 上的动点P(x,y),则y+|PQ|的最小值是( )
上的动点P(x,y),则y+|PQ|的最小值是( )