
科目:czsx 来源: 题型:013
如图,已知在等边△ABC中, ,连结
,连结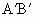 ,
,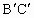 ,
,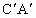 ,依据上述条件:(1)△
,依据上述条件:(1)△ ≌△
≌△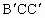 ≌△
≌△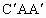 ;(2)△
;(2)△ 是等边三角形;(3)△
是等边三角形;(3)△ ≌△
≌△ .上述结论正确的是
.上述结论正确的是
[ ]
科目:czsx 来源:数学教研室 题型:013
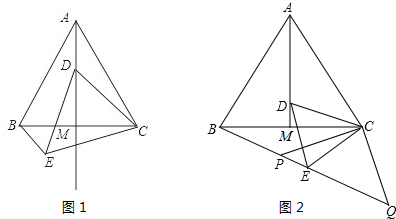
A.45° B.55°
C.60° D.75°
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| (n-2)180° |
| n |
| (n-2)180° |
| n |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源:2013年初中毕业升学考试(浙江衢州卷)数学(带解析) 题型:解答题
【提出问题】
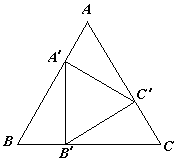
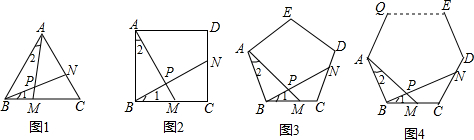
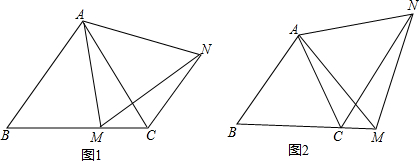
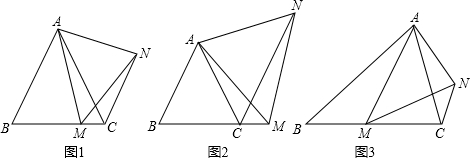
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.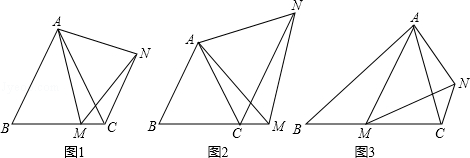
科目:czsx 来源:2013年初中毕业升学考试(浙江衢州卷)数学(解析版) 题型:解答题
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
科目:czsx 来源:2013-2014学年福建省福鼎市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
【提出问题】
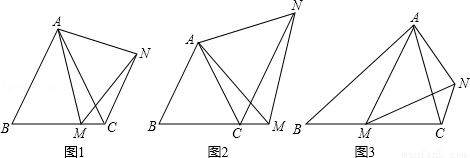
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
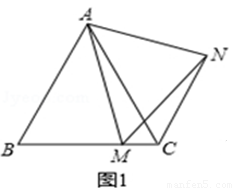
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
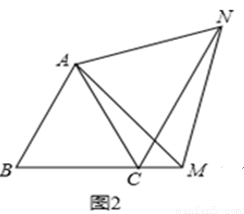
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
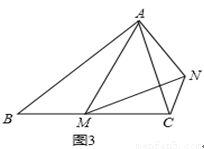
科目:czsx 来源:2013-2014学年河北省毕业生结课小模拟考试数学试卷(解析版) 题型:解答题
提出问题
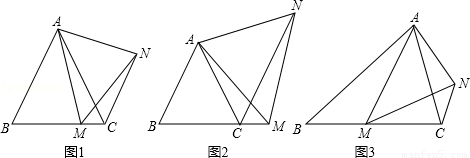
如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
类比探究
如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
拓展延伸
如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
【提出问题】
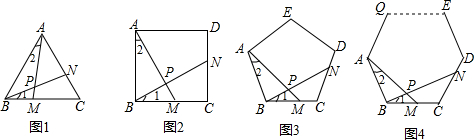
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

科目:czsx 来源:2013年浙江省衢州市高级中等学校招生考试数学 题型:044
提出问题
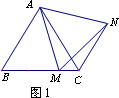
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
类比探究
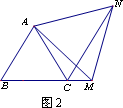
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
拓展延伸
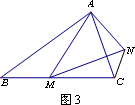
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的![]() 数量关系,并说明理由.
数量关系,并说明理由.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
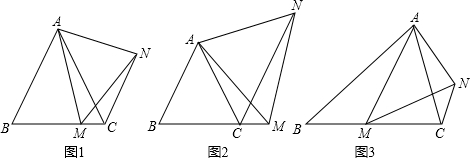
提出问题
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN. 求证:∠ABC=∠ACN.
类比探究
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
拓展延伸
(3)如图3,在等腰△ABC中, BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN =∠ABC. 连结CN. 试探究∠ABC与∠ACN的数量关系,并说明理由.

科目:czsx 来源: 题型:
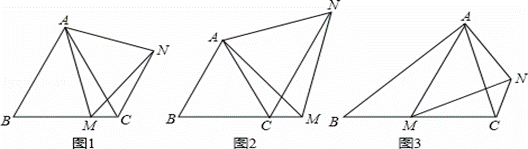
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
科目:czsx 来源:2013年浙江省衢州市中考数学试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
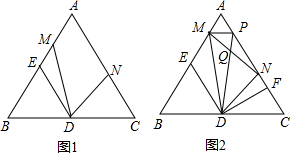 连DM,作DN平分∠MDC交AC于N.
连DM,作DN平分∠MDC交AC于N.