
科目:gzsx 来源:宁夏银川一中2012届高三第三次模拟考试数学理科试题 题型:044
已知点P是直角坐标平面内的动点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且![]() .
.
(Ⅰ)求动点P所在曲线C的方程;
(Ⅱ)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(Ⅲ)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使S![]() =λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
科目:gzsx 来源: 题型:
已知圆N的标准方程为
(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
科目:gzsx 来源: 题型:
| d2 |
| d1 |
| ||
| 2 |
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
科目:gzsx 来源: 题型:
| d2 |
| d1 |
| ||
| 2 |
| S | 2 2 |
科目:gzsx 来源:2011-2012学年重庆市高三第五次月考理科数学 题型:解答题
已知点P是直角坐标平面内的动点,点P到直线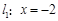 的距离为d1,到点F(–
1,0)的距离为d2,且
的距离为d1,到点F(–
1,0)的距离为d2,且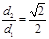 .
.
(1) 求动点P所在曲线C的方程;
(2)
直线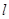 过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线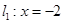 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为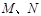 ,试判断点F与以线段
,试判断点F与以线段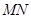 为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)
记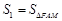 ,
,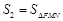 ,
,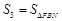 (A、B、
(A、B、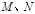 是(2)中的点),问是否存在实数
是(2)中的点),问是否存在实数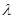 ,使
,使 成立.若存在,求出
成立.若存在,求出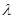 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:gzsx 来源:2012-2013学年江苏省南通市通州区高三(下)2月寒假调研数学试卷(解析版) 题型:解答题
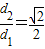 .
.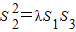 成立.若存在,求出λ的值;若不存在,请说明理由.
成立.若存在,求出λ的值;若不存在,请说明理由.科目:gzsx 来源:2011年上海市黄浦区高考数学二模试卷(理科)(解析版) 题型:解答题
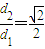 .
.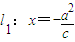 、点F(-c,0)、曲线C:
、点F(-c,0)、曲线C: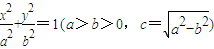 ,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).科目:gzsx 来源:2012-2013学年江苏省苏州市张家港市梁丰高级中学高三(上)期末数学模拟试卷(一)(解析版) 题型:解答题
 .
. 成立.若存在,求出λ的值;若不存在,请说明理由.
成立.若存在,求出λ的值;若不存在,请说明理由.科目:gzsx 来源:安徽省桐城十中2012届高三上学期第一次月考数学文科试题 题型:044
已知点P是直角坐标平面内的动点,点P到直线![]() (p是正常数)的距离为d1,到点
(p是正常数)的距离为d1,到点![]() 的距离为d2,且d1-d2=1.
的距离为d2,且d1-d2=1.
(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B,分别过A、B点作直线![]() 的垂线,对应的垂足分别为M、N,求证
的垂线,对应的垂足分别为M、N,求证![]() =0;
=0;
(3)记![]() ,
,![]() ,
,![]() (A、B、M、N是(2)中的点),
(A、B、M、N是(2)中的点),![]() ,求λ的值.
,求λ的值.
科目:gzsx 来源:浙江省宁波市鄞州区2012届高三高考适应性考试(3月)数学理科试题 题型:013
在Rt△ABC中,AC=2,BC=2,已知点P是△ABC内一点,则![]() ·(
·(![]() +
+![]() )的最小值是
)的最小值是
A.-2
B.-1
C.0
D.1
科目:gzsx 来源:2012-2013学年浙江省一级重点中学(六校)高三第一次联考数学试卷(理科)(解析版) 题型:填空题
 的最小值是 .
的最小值是 . 科目:gzsx 来源:2012年浙江省宁波市鄞州区高三3月适应性考试数学试卷(理科)(解析版) 题型:选择题
 的最小值是( )
的最小值是( )科目:gzsx 来源: 题型:
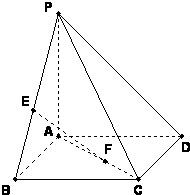 如图,已知点P是正方形ABCD所在平面外一点,PA⊥平面ABCD,PA=AB,点E、F分别在线段PB、AC上,满足BE=CF.
如图,已知点P是正方形ABCD所在平面外一点,PA⊥平面ABCD,PA=AB,点E、F分别在线段PB、AC上,满足BE=CF.科目:gzsx 来源:2010-2011年重庆市高二下学期检测数学试卷 题型:解答题
如图,已知点P是三角形ABC外一点,且 底面
底面
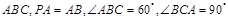 ,点
,点 ,
, 分别在棱
分别在棱 上,且
上,且 。
。
。
。
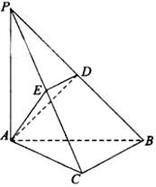
(1)求证: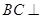 平面
平面 ;
;
(2)当 为
为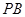 的中点时,求
的中点时,求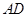 与平面
与平面 所成的角的大小;
所成的角的大小;
(3)是否存在点 使得二面角
使得二面角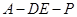 为直二面角?并说明理由.
为直二面角?并说明理由.
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型: