早三角形ABC中，角ABC=角ACB答案解析

科目：czsx 来源： 题型：

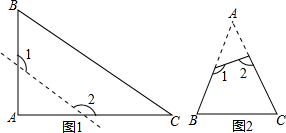
证明命题：“等腰三角形两底角的平分线相等．”是真命题．
已知：如图，在△ABC中，AB=

AC

AC

，BD，CE分别∠ABC，∠ACB的角平分线．
求证：

BD=CE

BD=CE

．
证明：

科目：czsx 来源： 题型：

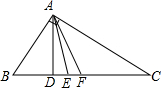如图，在直角三角形ABC中，AD为斜边上的垂线，AE为角平分线，AF为中线，
（1）证明：AF=BF=CF；
（2）写出∠FAE和∠DAE的关系并证明你的结论．

科目：czsx 来源： 题型：

如图，△ABC中，AC=BC，∠ACB=120°，点D在AB边上运动（D不与A、B重合），连接CD．作∠CDE=30°，DE交AC于点E．
（1）当DE∥BC时，△ACD的形状按角分类是

直角

直角

三角形；
（2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由．

科目：czsx 来源： 题型：

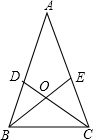等腰三角形ABC中，AB=AC，BE、CD分别是∠ABC、∠ACB的角平分线，且BE与CD交于O点，那么你能判断△OBC是什么三角形吗？
解：∵△ABC是等腰三角形，AB=AC
∴∠

 

=∠

 

（

 

）
∵BE、CD分别是∠ABC、∠ACB的角平分线
∴∠EBC=

1

2

∠

 

；∠DCB=

1

2

∠

 

∴∠

 

=∠

 

∴△OBC是

 

三角形（

 

）

科目：czsx 来源： 题型：

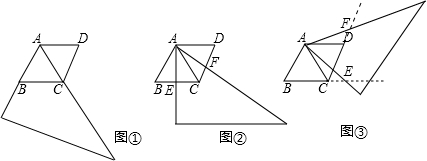
38、如图，在三角形ABC中，∠1=∠2，G为AD的中点，延长BG交AC于E．F为AB上的一点，CF⊥AD于H．下列判断正确的有（　　）
（1）AD是三角形ABE的角平分线；
（2）BE是三角形ABD边AD上的中线；
（3）CH为三角形ACD边AD上的高．

A、1个

B、2个

C、3个

D、0个

科目：czsx 来源： 题型：阅读理解

科目：czsx 来源： 题型：

如图，在三角形ABC中，AB=AC，AD垂直AB于A，角BAC等于120度，AD=3厘米．
求：BC的长．

科目：czsx 来源： 题型：

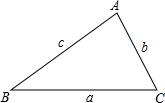（2007•东城区一模）我们给出如下定义：如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c．
（1）若∠A=2∠B，且∠A=60°，求证：a²=b（b+c）．
（2）如果对于任意的倍角三角形ABC（如图），其中∠A=2∠B，关系式a²=b（b+c）是否仍然成立？请证明你的结论；
（3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数．

科目：czsx 来源： 题型：阅读理解

（2012•大兴区一模）阅读下列材料：
小明遇到一个问题：已知：如图1，在△ABC中，∠BAC=120°，∠ABC=40°，试过△ABC的一个顶点画一条直线，将此三角形分割成两个等腰三角形．
他的做法是：如图2，首先保留最小角∠C，然后过三角形顶点A画直线交BC于点D．将∠BAC分成两个角，使∠DAC=20°，△ABC即可被分割成两个等腰三角形．
喜欢动脑筋的小明又继续探究：当三角形内角中的两个角满足怎样的数量关系时，此三角形一定可以被过顶点的一条直线分割成两个等腰三角形．
他的做法是：如图3，先画△ADC，使DA=DC，延长AD到点B，使△BCD也是等腰三角形，如果DC=BC，那么∠CDB=∠ABC，因为∠CDB=2∠A，所以∠ABC=2∠A．于是小明得到了一个结论：
当三角形中有一个角是最小角的2倍时，则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形．
请你参考小明的做法继续探究：当三角形内角中的两个角满足怎样的数量关系时，此三角形一定可以被过顶点的一条直线分割成两个等腰三角形．请直接写出你所探究出的另外两条结论（不必写出探究过程或理由）．

科目：czsx 来源： 题型：

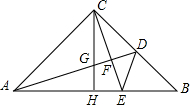如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．
（1）找出图中的全等三角形；
（2）找出与∠ADC相等的角，并请说明理由．

科目：czsx 来源： 题型：

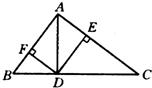6、如图，在直角三角形ABC中，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（除之C外）相等的角的个数是（　　）

A、2

B、3

C、4

D、5

科目：czsx 来源： 题型：

10、如图所示在三角形△ABC中AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论中，①AB上一点与AC上一点到D的距离相等；②AD上任意一点到AB、AC的距离相等；③∠BDE=∠CDF；④BD=CD，AD⊥BC．其中正确的个数是（　　）

A、1个

B、2个

C、3个

D、4个

科目：czsx 来源： 题型：

用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD．把一个含60°角的三角尺与这个菱形叠合，如果使三角尺60°角的顶点与点A重合，两边分别与AB、AC重合，将三角尺绕A点按逆时针方向旋转．
（1）当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时，通过观察或测量BE、CF的长度，你能得出什么结论？证明你的结论．
（2）当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F时，你在（1）中得到的结论还成立吗？简要说明理由．
（3）在（1）的图形中证明四边形AECF的面积等于菱形ABCD的面积的一半．

科目：czsx 来源： 题型：

如图①，用两个全等的等边三角形△ABC和△ACD拼成四边形ABCD，把一个含60°角的三角尺与四边形重叠，使60°角顶点与A重合，两边分别与AB，AC重合，现将三角形绕A点按逆时针方向旋转．
（1）当三角尺两边与BC，CD相交于E，F时（如图②），请判断∠BAE与∠CAF是否相等，请说明理由．
（2）在（1）的条件下，观察BE，CF的长度，你得到什么结论，请说明理由．
（3）当三角尺的两边与BC，CD的延长线相交于E，F时（如图③），（2）中的结论还成立吗？请说明理由．

科目：czsx 来源： 题型：

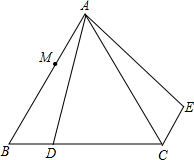如图，△ABC等边三角形，D是BC上一点，△ABD经过旋转后到达△ACE的位置．
（1）旋转中心是点

A

A

；
（2）旋转角最少是

60

60

度；
（3）如果点M是AB上的一点，那么经过上述旋转后，点M旋转到什么位置？请在图中将点M的对应点M′表示出来；
（4）如果AM=2，请计算点M旋转到M′过程中所走过的最短的路线长度（结果保留π）；
（5）如果等边三角形△ABC的边长为6，求四边形ADCE的面积．

科目：czsx 来源： 题型：

有四个同样大小边长为a的六角螺母如图所示排列，则图中三角形ABC的面积等于

 

．

科目：czsx 来源： 题型：

用两个全等且边长为4的等边三角形△ABC和△ACD拼成菱形ABCD．把一个60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合，将三角尺绕点A按逆时针方向旋转．
（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如图1），通过观察或测量BE，CF的长度，你能得出什么结论？（直接写出结论，不用证明）；
（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图2），你在（1）中得到的结论还成立吗？说明理由；
（3）在上述情况中，△AEC的面积是否会等于2

3

？如果能，求BE的长；如果不能，请说明理由．

科目：czsx 来源： 题型：

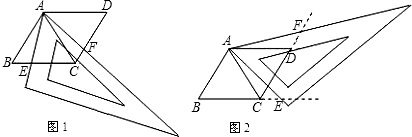
21、如图，点D是等边三角形ABC内的一点，将△BDC绕点C顺时针旋转60°，试画出旋转后的三角形，并指出图中的全等图形以及它们的对应顶点、对应边和对应角．

科目：czsx 来源： 题型：阅读理解

24、先阅读下面的材料，然后解答问题：
已知：如图1等腰直角三角形ABC中，∠B=90°，AD是角平分线，交BC边于点D．
求证：AC=AB+BD．
证明：如图1，在AC上截取AE=AB，连接DE，则由已知条件易知：Rt△ADB≌Rt△ADE（AAS）
∴∠AED=∠B=90°，DE=DB
又∵∠C=45°，∴△DEC是等腰直角三角形．
∴DE=EC．
∴AC=AE+EC=AB+BD．
我们将这种证明一条线段等于另两线段和的方法称为“截长法”．
解决问题：现将原题中的“AD是内角平分线，交BC边于点D”换成“AD是外角平分线，交BC边的延长线于点D，如图2”，其他条件不变，请你猜想线段AC、AB、BD之间的数量关系，并证明你的猜想．

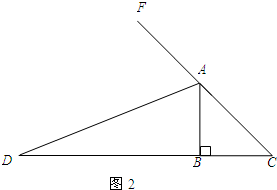
科目：czsx 来源： 题型：

学习了“多边形内角和”这一节后，老师给茗茗留了一道习题，请你帮茗茗完成．
（1）①如图，在△ABC中，∠A=90°，若沿图中虚线剪去∠A，则∠1+∠2的度数为

270°

270°

；②如图，在△ABC中，∠A=50°，剪去∠A后成四边形，则∠1+∠2的度数为

230°

230°

；③根据①与②的求解过程，请你猜想∠1+∠2与∠A的关系是

∠1+∠2=∠A+180°

∠1+∠2=∠A+180°

；
（2）在（1）中可以知道，一个三角形，通过剪去一个角将它变成四边形时，所得到的新的角和被剪去角之间的关系，如果剪去三角形的两个角，将它变成一个五边形时，剪去的两个角和新的角之间又有怎样的关系？剪去三角形的三个角，将它变成一个六边形时，剪去的三个角和新的角之间又有怎样的关系？
（3）如果将四边形剪去一个角变成五边形，剪去两个角变成六边形，剪去三个角变成七边形，所剪去的角和新角的关系是否与（2）中的相同？如果不同，请说明理由．