抛物线与x轴交于A(-2,0)B(4,0)与y轴交于C(0,-8)点C答案解析
科目:czsx
来源:
题型:
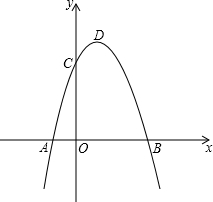
(2013•崇左)抛物线y=-x
2平移后的位置如图所示,点A,B坐标分别为(-1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.
(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
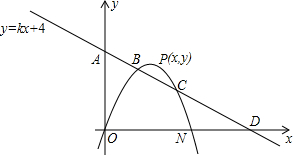
如图所示,抛物线y=ax
2+bx+c经过原点O,与x轴交于另一点N,直线y=kx+4与两坐标轴分别交于A、D两点,与抛物线交于B(1,m)、C(2,2)两点.
(1)求直线与抛物线的解析式;
(2)若抛物线在x轴上方的部分有一动点P(x,y),设∠PON=α,求当△PON的面积最大时tanα的值;
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△PO
A的面积等于△PON面积的
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=x2+px+q上有一点M(x0,y0)位于x轴下方.
(1)求证:此抛物线与x轴交于两点;
(2)设此抛物线与x轴的交点为A(x1,0),B(x2,0),且x1<x2,求证:x1<x0<x2.
查看答案和解析>>
科目:czsx
来源:
题型:
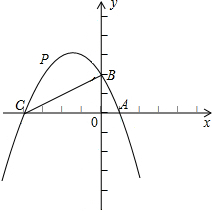
(2013•高要市一模)如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125).
(1)求抛物线的解析式;
(2)已知点P是抛物线上的一个动点,且在B、C两点之间,问当点P运动到什么位置时,△PBC的面积最大?并求出此时点P的坐标和△PBC的最大面积.
查看答案和解析>>
科目:czsx
来源:
题型:
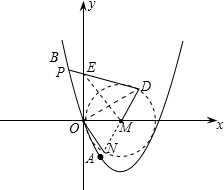
已知:如图,抛物线y=ax
2+bx+c经过原点(0,0)和A(1,-3)、B(-1,5)三点.
(1)求抛物线的解析式.
(2)设抛物线与x轴的另一个交点为C.以OC为直径作⊙M,如果过抛物线上一点P作⊙M的切线PD,切点为D,且y轴的正半轴交于点为E,连接MD.已知点E的坐标为(0,m),求四边形EOMD的面积.(用含m的代数式表示)
(3)延长DM交⊙M于点N,连接ON、OD,当点P在(2)的条件下运动到什么位置时,能使得S
四边形EOMD=S
△DON?请求出此时点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:抛物线y=-x
2+(m+2)x+m-1与x轴交于A、B两点(点A、B分别在原点O的左、右两侧),以OA、OB为直径作⊙O
1和⊙O
2.
(1)请问:⊙O
1和⊙O
2,能否为等圆?若能,求出其半径的长度;若不能,说明理由;
(2)设抛物线向上平移4个单位后,⊙O
1、⊙O
2的面积分别成为S
1、S
2,且4S
2-16S
1=5π,求平移后所得抛物线的解析式;
(3)由(2)所得的抛物线与y轴交于点C,⊙O
1和⊙O
2的一条外公切线MN分别交x轴和y轴

于点P、Q(M、N为切点,如图所示),求△CPQ的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c的对称轴是x=1,并且经过(-2,-5)和(5,-12)两点.
(1)求此抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C 点,D是线段BC上一点(不与点B、C重合),若以B、O、D为顶点的三角形与△BAC相似,求点D的坐标;
(3)点P在y轴上,点M在此抛物线上,若要使以点P、M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
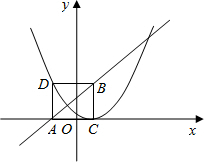
如图,已知点B(1,3),C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD.
(1)填空:A点坐标为(
,
),D点坐标为(
,
);
(2)若抛物线y=
x
2+bx+c经过C,D两点,求抛物线的解析式;
(3)将(2)中的抛物线沿y轴向上平移,设平移后所得抛物线与y轴交点为E,点M是平移后的抛物线与直线AB的公共点,在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.
(提示:抛物线y=ax
2+bx+c(a≠0)的对称轴是x=-
,顶点坐标是(-
,
)
查看答案和解析>>
科目:czsx
来源:
题型:

如图,直线y=x+m和抛物线y=x
2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为C,与y轴交于点D,求四边形ABCD的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
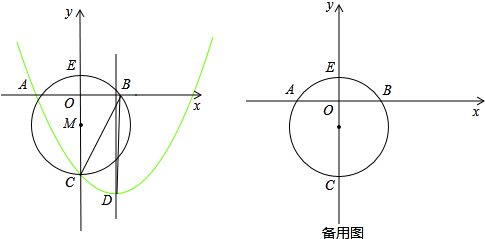
如图,在平面直角坐标系中,有点M(0,-3),⊙M与x轴交于点A、B(点A在点 B的左侧),与y轴交于点C、E;抛物线y=ax
2+bx-8(a≠0)经过A、C两点,点D是抛物线的顶点;
(1)求点A、B、C的坐标;
(2)试探究:当a取何值时,抛物线y=ax
2+bx-8(a≠0)的对称轴与⊙M相切?
(3)当点D在第四象限内时,连接BC、BD,且
tan∠CBD=.
①试确定a的值;
②设此时的抛物线与x轴的另一个交点是点F,在抛物线的对称轴上找一点T,使|TM-TF|达到最大,请求出最大值与点T的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

已知二次函数y=mx
2+(m-3)x-3 (m>0)
(1)求证:它的图象与x轴必有两个不同的交点;
(2)这条抛物线与x轴交于A(x
1,0)和B(x
2,0)(x
1<x
2),与y轴交于点C,且AB=4,⊙M过A、B、C三点,求扇形MAC的面积S;
(3)在(2)的条件下,抛物线上是否存在点P使△PBD(PD垂直于x轴,垂足为D)被直线BC分成面积比为1:2的两部分?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线y=
x
2-2x+1的顶点为P,A为抛物线与y轴的交点,过A与y轴垂直的直线与抛物线的另一交点为B,与抛物线对称轴交于点O′,过点B和P的直线l交y轴于点C,连接O′C,将△ACO′沿O′C翻折后,点A
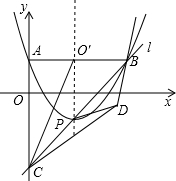
落在点D的位置.
(1)求直线l的函数解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点Q,使得S
△DQC=S
△DPB?若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
己知:抛物线y=x
2-(k+1)x+k
(1)试求k为何值时,抛物线与x轴只有一个公共点;
(2)如图,若抛物线与x轴交于A,B两点(点A在点B的左边),与y轴的负半轴交于点C,
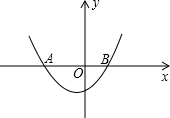
试问:是否存在实数k,使△AOC与△COB相似?若存在,求出相应的k的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2011•同安区质检)已知抛物线y=x2-mx+m-2;
(1)求证:抛物线y=x2-mx+m-2与x轴有两个不同的交点;
(2)若m是整数,抛物线y=x2-mx+m-2与x轴交于整数点,求m的值;
(3)在(2)的条件下,设抛物线的顶点为A,抛物线与x轴的两个交点中右侧交点为B.在坐标轴上是否存在一点M,使得△MAB为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
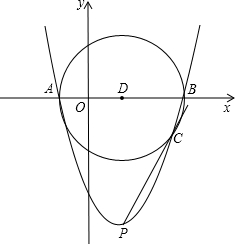
(2013•绍兴模拟)如图,抛物线与x轴交于A,B两点,点B坐标为(3,0)顶点P的坐标为(1,-4),以AB为直径作圆,圆心为D,过P向右侧作⊙D的切线,切点为C.
(1)求抛物线的解析式;
(2)请通过计算判断抛物线是否经过点C;
(3)设M,N 分别为x轴,y轴上的两个动点,当四边形PNMC的周长最小时,请直接写出M,N两点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•莒南县一模)已知,如图二次函数y=ax
2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m),
(1)求二次函数的解析式并写出D点坐标;
(2)点Q是线段AB上的一动点,过点Q作QE∥AD交BD于E,连结DQ,当△DQE的面积最大时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:
已知开口向下的抛物线y=ax
2+bx+c与x轴交于M,N两点(点N在点M的右侧),并且M和N两点的横坐标分别是方程x
2-2x-3=0的两根,点K是抛物线与y轴的交点,∠MKN不小于90度.
(1)求点M和N的坐标;
(2)求系数a的取值范围;
(3)当y取得最大值时,抛物线上是否存在点P,使得
S△MPN=2?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

抛物线y=ax
2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
(1)根据图象所给信息,求出抛物线的解析式;
(2)求直线BC与y轴交点D的坐标;
(3)点P是直线BC上的一点,且△APB与△DOB相似,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
.
查看答案和解析>>
科目:czsx
来源:
题型:
如果抛物线y=-x2+2(m-1)x+m+1与x轴都交于A,B两点,且A点在x轴的正半轴上,B点在x轴的负半轴上,OA的长是a,OB的长是b.
(1)求m的取值范围;
(2)若a:b=3:1,求m的值,并写出此时抛物线的解析式;
(3)设(2)中的抛物线与y轴交于点C,抛物线的顶点是M,问:抛物线上是否存在点P,使△PAB的面积等于△BCM面积的8倍?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>

 (2013•崇左)抛物线y=-x2平移后的位置如图所示,点A,B坐标分别为(-1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.
(2013•崇左)抛物线y=-x2平移后的位置如图所示,点A,B坐标分别为(-1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D. A的面积等于△PON面积的
A的面积等于△PON面积的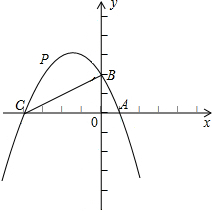 (2013•高要市一模)如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125).
(2013•高要市一模)如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125). 已知:如图,抛物线y=ax2+bx+c经过原点(0,0)和A(1,-3)、B(-1,5)三点.
已知:如图,抛物线y=ax2+bx+c经过原点(0,0)和A(1,-3)、B(-1,5)三点. 于点P、Q(M、N为切点,如图所示),求△CPQ的面积.
于点P、Q(M、N为切点,如图所示),求△CPQ的面积.  如图,已知点B(1,3),C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD.
如图,已知点B(1,3),C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
 已知二次函数y=mx2+(m-3)x-3 (m>0)
已知二次函数y=mx2+(m-3)x-3 (m>0) 落在点D的位置.
落在点D的位置. 试问:是否存在实数k,使△AOC与△COB相似?若存在,求出相应的k的值;若不存在,请说明理由.
试问:是否存在实数k,使△AOC与△COB相似?若存在,求出相应的k的值;若不存在,请说明理由.  (2013•绍兴模拟)如图,抛物线与x轴交于A,B两点,点B坐标为(3,0)顶点P的坐标为(1,-4),以AB为直径作圆,圆心为D,过P向右侧作⊙D的切线,切点为C.
(2013•绍兴模拟)如图,抛物线与x轴交于A,B两点,点B坐标为(3,0)顶点P的坐标为(1,-4),以AB为直径作圆,圆心为D,过P向右侧作⊙D的切线,切点为C.
 抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C, (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是