
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 1 |
| 2 |
科目:gzsx 来源: 题型:
|
|
科目:gzsx 来源: 题型:
| n | 2 |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源:2010-2011学年江西省吉安市高三最后一次模拟考试理科数学 题型:解答题
(本小题满分14分)已知数列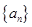 是以d为公差的等差数列,数列
是以d为公差的等差数列,数列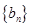 是以q为公比的
是以q为公比的
等比数列。
(1)若数列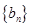 的前n项和为
的前n项和为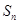 且
且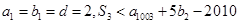 ,求整数q的值;
,求整数q的值;
(2)在(1)的条件下,试问数列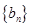 中最否存在一项
中最否存在一项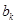 ,使得
,使得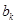 恰好可以表示为该数列
恰好可以表示为该数列
中连续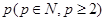 项的和?请说明理由;
项的和?请说明理由;
(3)若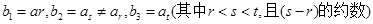 ,求证:数列
,求证:数列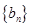
中每一项都是数列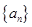 中的项。
中的项。
科目:gzsx 来源: 题型:
(07年湖南卷文)(13分)
设![]() ,
,
![]() .
.
(Ⅰ)证明数列![]() 是常数数列;
是常数数列;
(Ⅱ)试找出一个奇数![]() ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列![]() 中的所有项都是数列
中的所有项都是数列![]() 中的项,并指出
中的项,并指出![]() 是数列
是数列![]() 中的第几项.
中的第几项.
科目:gzsx 来源:2012届福建省四地六校联考上学期高三第三次月考理科数学试卷 题型:解答题
已知成等差数列的三个正数的和为15,并且这三个数分别加上2、5、13后成为等比数列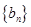 中的
中的
(1) 求数列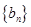 的通项公式;
的通项公式;
(2) 数列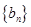 的前n项和为
的前n项和为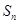 ,求证:数列
,求证:数列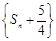 是等比数列.
是等比数列.
科目:gzsx 来源:2011-2012学年上海市徐汇区高三4月学习能力诊断理科数学试卷(解析版) 题型:解答题
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数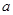 使得数列
使得数列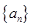 满足:若
满足:若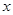 是数列
是数列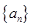 中的一项,则
中的一项,则 也是数列
也是数列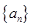 中的一项,称数列
中的一项,称数列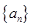 为“兑换数列”,常数
为“兑换数列”,常数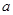 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: 是“兑换系数”为
是“兑换系数”为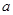 的“兑换数列”,求
的“兑换数列”,求 和
和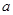 的值;
的值;
(2)已知有穷等差数列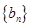 的项数是
的项数是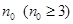 ,所有项之和是
,所有项之和是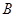 ,求证:数列
,求证:数列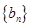 是“兑换数列”,并用
是“兑换数列”,并用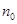 和
和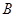 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列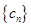 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
科目:gzsx 来源:2011-2012学年山东省高三下学期模拟预测文科数学试卷(解析版) 题型:选择题
由命题p:“函数y=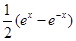 是奇函数”,与命题q:“数列a,a2,a3,…,
a n,…是等比数列”构成的复合命题中,下列判断正确的是( )
是奇函数”,与命题q:“数列a,a2,a3,…,
a n,…是等比数列”构成的复合命题中,下列判断正确的是( )
A.p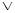 q为假,p
q为假,p q为假 B.p
q为假 B.p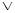 q为真,p
q为真,p q为真
q为真
C.p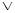 q为真,p
q为真,p q为假 D.p
q为假 D.p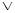 q为假,p
q为假,p q为真
q为真
科目:gzsx 来源:2011-2012学年陕西省高三开学第一次考试理科数学 题型:解答题
(12分)成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13
后成为等比数列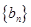 中的
中的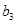 、
、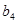 、
、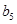 .
.
(1) 求数列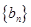 的通项公式;
的通项公式;
(2) 数列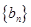 的前n项和为
的前n项和为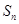 ,求证:数列
,求证:数列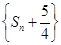 是等比数列.
是等比数列.
科目:gzsx 来源: 题型:
(09年湖北重点中学联考理)(13分)
已知数列![]() 的通项公式是
的通项公式是![]() ,数列
,数列![]() 是等差数列,令集合
是等差数列,令集合![]() ,
,![]() ,
,![]() .将集合
.将集合![]() 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前5项成等比数列,且
的前5项成等比数列,且![]() ,
,![]() .
.
(i)求证:元素2不可能是数列![]() 中的第
中的第![]() 项(
项(![]() )
)
科目:gzsx 来源:2007年普通高等学校招生全国统一考试文科数学卷(湖南) 题型:解答题
(本小题满分13分)
设 是数列
是数列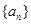 (
( )的前
)的前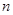 项和,
项和,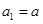 ,且
,且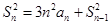 ,
, ,
,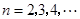 .
.
(I)证明:数列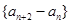 (
(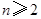 )是常数数列;
)是常数数列;
(II)试找出一个奇数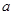 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列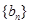 (
( )中的所有项都是数列
)中的所有项都是数列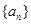 中的项,并指出
中的项,并指出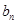 是数列
是数列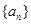 中的第几项.
中的第几项.
科目:gzsx 来源: 题型:
(本小题满分16分)已知数列![]() 是以
是以![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,求整数
,求整数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续![]() 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若![]() (其中
(其中![]() ,且(
,且(![]() )是(
)是(![]() )的约数),求证:数列
)的约数),求证:数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项.
中的项.
科目:gzsx 来源:2007年普通高等学校招生全国统一考试文科数学卷(湖南) 题型:解答题
(本小题满分13分)
设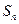 是数列
是数列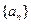 (
(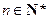 )的前
)的前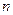 项和,
项和, ,且
,且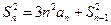 ,
, ,
,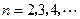 .
.
(I)证明:数列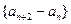 (
(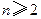 )是常数数列;
)是常数数列;
(II)试找出一个奇数 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列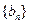 (
(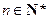 )中的所有项都是数列
)中的所有项都是数列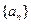 中的项,并指出
中的项,并指出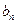 是数列
是数列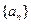 中的第几项.
中的第几项.
科目:gzsx 来源:2011-2012学年浙江省高三第二次五校联考理科数学试卷(解析版) 题型:解答题
(本题满分14分) 设公比为正数的等比数列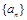 的前
的前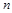 项和为
项和为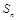 ,已知
,已知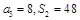 ,数列
,数列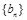 满足
满足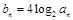 .
.
(Ⅰ)求数列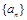 和
和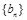 的通项公式;
的通项公式;
(Ⅱ)是否存在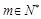 ,使得
,使得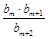 是数列
是数列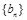 中的项?若存在,求出
中的项?若存在,求出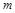 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.