精英家教网 >
试题搜索列表 >已知函数f(x)=ax2-blnx在点(1,f(1))处的切线方程为y=3x-1(1)若f(x)在定义域里的一个子区间(k-1,k+1)内不是单调函数
已知函数f(x)=ax2-blnx在点(1,f(1))处的切线方程为y=3x-1(1)若f(x)在定义域里的一个子区间(k-1,k+1)内不是单调函数答案解析
科目:gzsx
来源:福建省漳州三中2010-2011学年高三第二次月考数学(理)
题型:解答题
已知函数 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值所组成的集合A;
(Ⅱ)设关于x的方程 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式 对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由?
查看答案和解析>>
科目:gzsx
来源:
题型:
(09年海淀区期末理)(12分)
已知函数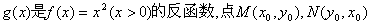 分别是
分别是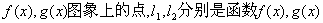 的图象在M、N两点处的切线,且
的图象在M、N两点处的切线,且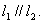
(1)求M、N两点的坐标;
(2)求经过点O、M、N的圆的方程(O是坐标原点)。
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•南宁模拟)已知函数f(x)=x
4-x
3+ax
2-1在区间(0,2)单调递减,在区间(2,3)单调递增.
(Ⅰ)求a的值;
(Ⅱ)已知函数
g(x)=3x3-(9-b)x2-1(b<-),求证:g(x)与函数f(x)的图象恰有1个交点.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
2+lnx(a∈R).
(1)当a=
时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f
1(x),f
2(x),在公共定义域D上,满足f
1(x)<g(x)<f
2(x),那么就称g(x)为f
1(x),f
2(x)的“活动函数”.已知函数
f1(x)=(a-)x2+2ax+(1-a2)lnx,f2(x)=x2+2ax.若在区间(1,+∞)上,函数f(x)是f
1(x),f
2(x)的“活动函数”,求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
2+lnx(a∈R).
(1)当
a=时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f1(x),f2(x),在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称为g(x)为f
1(x),f
2(x)的“活动函数”.
已知函数
f1(x)=(a-)x2+2ax+(1-a2)lnx,
f2(x)=x2+2ax.
①若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围;
②当
a=时,求证:在区间(1,+∞)上,函数f1(x),f2(x)的“活动函数”有无穷多个.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•日照一模)已知函数f(x)=ax
2+1nx(a∈R).
(Ⅰ)当
a=时,求f(x)在区间[1,e]上的最大值和最小值;
(Ⅱ)如果在公共定义域D上的函数g(x),f
1(x),f
2(x)满足f
1(x)<g(x)<f
2(x),那么就称g(x)为f
1(x)、f
2(x)的“活动函数”,已知函数
f1(x)=(a-)x2+2ax+(1-a2)lnx,
f2(x)=x2+2ax,若在区间(1,+∞)上,函数f(x)是f
1(x)、f
2(x)的“活动函数”,求实数a的取范围.
查看答案和解析>>
科目:gzsx
来源:南宁模拟
题型:解答题
已知函数f(x)=x
4-x
3+ax
2-1在区间(0,2)单调递减,在区间(2,3)单调递增.
(Ⅰ)求a的值;
(Ⅱ)已知函数
g(x)=3x3-(9-b)x2-1(b<-),求证:g(x)与函数f(x)的图象恰有1个交点.
查看答案和解析>>
科目:gzsx
来源:福建省安溪一中、惠安一中、养正中学2011-2012学年高一上学期期中联考数学试题
题型:044
若函数f(x)满足下列条件:在定义域内存在x0,使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)具有性质M;反之,若x0不存在,则称函数f(x)不具有性质M.
(Ⅰ)证明:函数f(x)=2x具有性质M,并求出对应的x0的值;
(Ⅱ)已知函数h(x)=lg 具有性质M,求a的取值范围;
具有性质M,求a的取值范围;
(Ⅲ)试探究形如①y=kx+b(k≠0)、②y=ax2+bx+c(a≠0)、③y= (k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.
(k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.
查看答案和解析>>
科目:gzsx
来源:河南省期中题
题型:解答题
已知函数g(x)=ax2-4x+3的递增区间是(-∞,-2)。
(1)求a的值;
(2)设f(x)=g(x-2),求f(x)在区间[-3,2]上的最大值和最小值。
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知函数f(x)=ax
2+lnx(a∈R).
(1)当
a=时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f
1(x),f
2(x),在公共定义域D上,满足f
1(x)<g(x)<f
2(x),那么就称g(x)为f
1(x),
f
2(x)的“活动函数”.
已知函数
f1(x)=(a-)x2+2ax+(1-a2)lnx,f2(x)=x2+2ax.
若在区间(1,+∞)上,函数f(x)是f
1(x),f
2(x)的“活动函数”,
求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
(1)求函数y=3ex+xsinx的导数;
(2)已知函数y=lnx+ax2+bx在x=1和x=2处有极值,求实数a,b的值.
查看答案和解析>>
科目:gzsx
来源:2010年内蒙古包头市高一上学期期中考试数学试卷
题型:解答题
(12分) 已知函数 是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
查看答案和解析>>
科目:gzsx
来源:
题型:022
已知函数g ( x ) = ax2 +bx + c(a≠0)的图像如图所示.那么对 f ( x ) = a-|1-x|,把f ( 5 ),f (-2),f ( 0.5 )从小到大排列起来的结果是__________________________.

查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知函数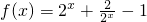 ,x∈[0,+∞)
,x∈[0,+∞)
(1)证明:函数在 上为单调减函数,在
上为单调减函数,在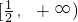 上为单调增函数;
上为单调增函数;
(2) 若x∈[0,a],求f(x)的最大最小值.
查看答案和解析>>
科目:gzsx
来源:数学教研室
题型:022
已知函数g ( x ) = ax2 +bx + c(a≠0)的图像如图所示.那么对 f ( x ) = a-|1-x|,把f ( 5 ),f (-2),f ( 0.5 )从小到大排列起来的结果是__________________________.
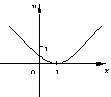
查看答案和解析>>
科目:gzsx
来源:山东省博兴二中2008届高三第一次月考(数学理)新人教版
题型:044
查看答案和解析>>

 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数. 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式 对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由? ![]() 分别是
分别是![]() 的图象在M、N两点处的切线,且
的图象在M、N两点处的切线,且![]()
![]() 具有性质M,求a的取值范围;
具有性质M,求a的取值范围;![]() (k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.
(k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.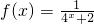 (x∈R).
(x∈R).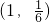 在f(x)的图象上,判断其关于点
在f(x)的图象上,判断其关于点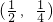 对称的点是否仍在f(x)的图象上;
对称的点是否仍在f(x)的图象上;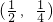 对称;
对称;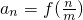 (m∈{N}^{*},n=1,2,…,m),求数列{an}的前m项和Sm.
(m∈{N}^{*},n=1,2,…,m),求数列{an}的前m项和Sm. 是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
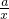 旦(a>0)有如下的性质:在区间(0,
旦(a>0)有如下的性质:在区间(0,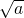 ]上单调递减,在[
]上单调递减,在[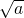 ,+∞)上单调递增.
,+∞)上单调递增.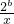 在(0,4]上单调递减,在[4,+∞)上单调递增,求常数b的值.
在(0,4]上单调递减,在[4,+∞)上单调递增,求常数b的值.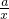 在x∈[l,2]的最大值.
在x∈[l,2]的最大值.
![]() ,x∈[
,x∈[![]() ,
,![]() ],
],![]() ∈(
∈(![]() ,
,![]() ).
).![]() =
=![]() 时,求函数f(x)的最大值与最小值;
时,求函数f(x)的最大值与最小值;![]() 的取值范围,使y=f(x)在区间[-1,
的取值范围,使y=f(x)在区间[-1,![]() ]上是单调函数.
]上是单调函数.