三角形有一个内角为60°,夹这个角的两边长分别为8和5,则它的内切圆面积答案解析
科目:gzsx
来源:
题型:
若三角形中有一个角为60°,夹这个角的两边的边长分别是8和5,则它的外接圆半径等于
.
查看答案和解析>>
科目:gzsx
来源:
题型:
三角形有一个角为60°,夹这个角的两边长分别为8和5,则这个三角形内切圆的面积为
_____________________________.
查看答案和解析>>
科目:gzsx
来源:月考题
题型:填空题
若三角形中有一个角为60 °,夹这个角的两边的边长分别是8和5,则它的外接圆半径等于( )
查看答案和解析>>
科目:gzsx
来源:同步题
题型:填空题
若三角形中有一个角为60°,夹这个角的两边的边长分别是8和5,则它的内切圆半径等于( ),外接圆半径等于( )。
查看答案和解析>>
科目:gzsx
来源:
题型:
若三角形中有一个角为60°,夹这个角的两边的边长分别是8和5,则它的外接圆半径等于________.
查看答案和解析>>
科目:gzsx
来源:同步题
题型:填空题
若三角形中有一个角为60°,夹这个角的两边的边长分别是8和5,则它的内切圆半径=( ),外接圆半径=( )。
查看答案和解析>>
科目:gzsx
来源:吉林省长春外国语学校09-10学年高二上学期第一次月考
题型:填空题
三角形中有一个角为60度,夹这个角的两边长分别为8和5,则这个三角形内切圆的面积为
查看答案和解析>>
科目:gzsx
来源:
题型:
三角形有一个角是60°,夹这个角的两边的长度分别为8和5,则此三角形内切圆的面积为( )
查看答案和解析>>
科目:gzsx
来源:
题型:单选题
三角形有一个角是60°,夹这个角的两边的长度分别为8和5,则此三角形内切圆的面积为
- A.
3π
- B.
6π
- C.
12π
- D.

π
查看答案和解析>>
科目:gzsx
来源:
题型:
(2007•上海模拟)(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为
arccos,周长为定值p,求面积S的最大值;
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S
2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)
2-c
2][c
2-(a-b)
2]=-c
4+2(a
2+b
2)c
2-(a
2-b
2)
2=-[c
2-(a
2+b
2)]
2+4a
2b
2而-[c
2-(a
2+b
2)]
2≤0,a
2≤81,b
2≤64,则S≤36,但是,其中等号成立的条件是c
2=a
2+b
2,a=9,b=8,于是c
2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S
2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
查看答案和解析>>
科目:gzsx
来源:
题型:
(2005•上海模拟)(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为
arccos,周长为定值p,求面积S的最大值;
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:
S=absinC≤×9×8sinC=36sinC,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a9,b8,c4时该三角形面积最大,此时
cosC=,
sinC=,所以,该三角形面积的最大值是
.以上解答是否正确?若不正确,请你给出正确的解答.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年陕西省高三高考模拟考试(八)文科数学试卷(解析版)
题型:选择题
“三角形有一个内角为 ”是“三内角成等差数列”的( )
”是“三内角成等差数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:gzsx
来源:2006-2007学年上海市十校高三联考数学试卷(理科)(解析版)
题型:解答题
(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为

,周长为定值p,求面积S的最大值;
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S
2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)
2-c
2][c
2-(a-b)
2]=-c
4+2(a
2+b
2)c
2-(a
2-b
2)
2=-[c
2-(a
2+b
2)]
2+4a
2b
2而-[c
2-(a
2+b
2)]
2≤0,a
2≤81,b
2≤64,则S≤36,但是,其中等号成立的条件是c
2=a
2+b
2,a=9,b=8,于是c
2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S
2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
查看答案和解析>>
科目:gzsx
来源:上海模拟
题型:解答题
(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为
arccos,周长为定值p,求面积S的最大值;
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:
S=absinC≤×9×8sinC=36sinC,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a9,b8,c4时该三角形面积最大,此时
cosC=,
sinC=,所以,该三角形面积的最大值是
.以上解答是否正确?若不正确,请你给出正确的解答.
查看答案和解析>>
科目:gzsx
来源:2004-2005学年上海市十校高三联考数学试卷(文科)(解析版)
题型:解答题
(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为

,周长为定值p,求面积S的最大值;
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:

,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a9,b8,c4时该三角形面积最大,此时

,
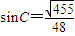
,所以,该三角形面积的最大值是

.以上解答是否正确?若不正确,请你给出正确的解答.
查看答案和解析>>
科目:gzsx
来源:2004-2005学年上海市十校高三联考数学试卷(理科)(解析版)
题型:解答题
(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为

,周长为定值p,求面积S的最大值;
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S
2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)
2-c
2][c
2-(a-b)
2]=-c
4+2(a
2+b
2)c
2-(a
2-b
2)
2=-[c
2-(a
2+b
2)]
2+4a
2b
2而-[c
2-(a
2+b
2)]
2≤0,a
2≤81,b
2≤64,则S≤36,但是,其中等号成立的条件是c
2=a
2+b
2,a=9,b=8,于是c
2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S
2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
查看答案和解析>>
科目:gzsx
来源:黄冈重点作业·高三数学(下)
题型:022
一面积为10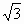 三角形,有一内角为
三角形,有一内角为 ,夹这个角的两边比为5∶2,则三角形内切圆半径为________.
,夹这个角的两边比为5∶2,则三角形内切圆半径为________.
查看答案和解析>>
科目:gzsx
来源:
题型:022
已知关于x的方程5x2-10xsinα+13sinα-6=0有两相等实根,其中α是平行四边形的一个内角,夹这个角的两边之和是6,则这个平行四边形面积的最大值是________(用分数表示)
查看答案和解析>>
科目:gzsx
来源:2010年广东省高二上学期第一次段考理科数学卷
题型:填空题
一个正四棱台形油槽可以装煤油190升,已知它的上下底边长分别等于60cm和40cm,则它的深度为________.
查看答案和解析>>
科目:gzsx
来源:
题型:填空题
一个正四棱台形油槽可以装煤油190升,已知它的上下底边长分别等于60cm和40cm,则它的深度为________.
查看答案和解析>>

 ”是“三内角成等差数列”的( )
”是“三内角成等差数列”的( ) ,周长为定值p,求面积S的最大值;
,周长为定值p,求面积S的最大值; ,周长为定值p,求面积S的最大值;
,周长为定值p,求面积S的最大值; ,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a9,b8,c4时该三角形面积最大,此时
,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a9,b8,c4时该三角形面积最大,此时 ,
,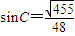 ,所以,该三角形面积的最大值是
,所以,该三角形面积的最大值是 .以上解答是否正确?若不正确,请你给出正确的解答.
.以上解答是否正确?若不正确,请你给出正确的解答. ,周长为定值p,求面积S的最大值;
,周长为定值p,求面积S的最大值;