已知正方体ABCD-A1B1C1D1的棱长为a,长为定值的线段EF答案解析
科目:gzsx
来源:
题型:

如图,已知正方体ABCD-A
1B
1C
1D
1,棱长为4,E为面A
1D
1DA的中心,
CF=3FC
1,AH=3HD,
(1)求异面直线EB
1与HF之间的距离
(2)求二面角H-B
1E-A
1的平面角的余弦值.
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,已知正方体ABCD—A
1B
1C1D
1中,棱长为a,M和N分别为棱AA
1和CC
1上的动点,且AM=C
1N.

(1)证明四边形BND1M是平行四边形;
(2)求四边形BND1M面积的最小值.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年湖北省武汉市华中师大一附中高二(下)期中数学试卷(理科)(解析版)
题型:解答题
如图,已知正方体ABCD-A
1B
1C
1D
1,棱长为4,E为面A
1D
1DA的中心,
CF=3FC
1,AH=3HD,
(1)求异面直线EB
1与HF之间的距离
(2)求二面角H-B
1E-A
1的平面角的余弦值.

查看答案和解析>>
科目:gzsx
来源:同步题
题型:解答题
如图所示,已知正方体ABCD- A
1B
1C
1D
1,棱长为a,在正方体内随机取一点P,求:
(1)点P到面ABCD的距离大于

的概率P
1;
(2)点P到面ABCD及面A
1B
1C
1D
1的距离都大于
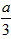
的概率P
2。
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
 如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
CF=3FC1,AH=3HD,
(1)求异面直线EB1与HF之间的距离
(2)求二面角H-B1E-A1的平面角的余弦值.
查看答案和解析>>
科目:gzsx
来源:
题型:
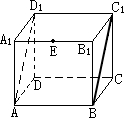
1、已知正方体ABCD-A
1B
1C
1D
1的棱长均为1,对于下列结论:
(1)BD
1⊥平面A
1DC
1;
(2)A
1C
1和AD
1所成角为45°;
(3)点A和点C
1在该正方体外接球表面上的球面距离为
π;
(4)E到平面ABC
1的距离为
(E为A
1B
1中点)
其中正确的结论个数是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
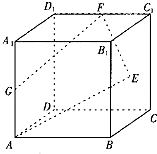
如图,已知正方体ABCD-A
1B
1C
1D
1的棱长为2,点E是正方形BCC
1B
1的中心,点F.G分别是棱C
1D
1,AA
1的中点.设点E
1,G
1分别是点E,G在平面DCC
1D
1内的正投影.
(1)证明:直线FG
1⊥平面FEE
1;
(2)求异面直线E
1G
1与EA所成角的正弦值.
(3)求四面体FGAE的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A1B1C1D1的棱长为2,线段EF在棱A1B1上移动,点P,Q分别在棱AD,CD上移动,若EF=1,PD=x,A1E=y,CQ=z,则三棱锥Q-PEF的体积( )
查看答案和解析>>
科目:gzsx
来源:
题型:
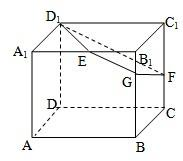
如图,已知正方体ABCD-A
1B
1C
1D
1的棱长为2,E、F分别是A
1B
1、CC
1的中点,过D
1、E、F作平面D
1EGF交BB
1于G.
(Ⅰ)求证:EG∥D
1F;
(Ⅱ)求二面角C
1-D
1E-F的余弦值;
(Ⅲ)求正方体被平面D
1EGF所截得的几何体ABGEA
1-DCFD
1的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A1B1C1D1的棱长为 a,求棱A1B1所在的直线与对角线B D1所在直线间的距离.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A
1B
1C
1D
1的棱长为2,P,Q分别BC,CD上的动点,
|PQ|=,确P,Q的位置,使QB
1⊥PD
1.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A
1B
1C
1D
1 的棱长为1,E为棱AA
1的中点,一直线过E点与异面直线BC,C
1D
1分别相交于M,N两点,则线段MN的长等于
3
3
.
查看答案和解析>>
科目:gzsx
来源:
题型:
25、已知正方体ABCD-A
1B
1C
1D
1的棱长为1,E,F,G分别是AB,BC,B
1C
1的中点.下列命题正确的是
②③④
(写出所有正确命题的编号).
①以正方体的顶点为顶点的三棱锥的四个面最多只有三个面是直角三角形;
②P在直线FG上运动时,AP⊥DE;
③Q在直线BC
1上运动时,三棱锥A-D
1QC的体积不变;
④M是正方体的面A
1B
1C
1D
1内到点D和 C
1距离相等的点,则M点的轨迹是一条线段.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2010•合肥模拟)已知正方体ABCD-A
1B
1C
1D
1的棱长为2,E、F、G分别是AB、BC、B
1C
1的中点.下列说法正确的是
①②③
①②③
(写出所有正确命题的编号).
①P在直线EF上运动时,GP始终与平面AA
1C
1C平行;
②点Q在直线BC
1上运动时,三棱锥A-D
1QC的体积不变;
③点M是平面A
1B
1C
1D
1上到点D和C
1距离相等的点,则点M的轨迹是一条的直线;
④以正方体ABCD-A
1B
1C
1D
1的任意两个顶点为端点连一条线段,其中与棱AA
1异面的有10条.
查看答案和解析>>
科目:gzsx
来源:
题型:
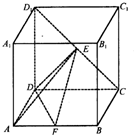
如图,已知正方体ABCD-A
1B
1C
1D
1的棱长为2,E、F分别是D
1C、AB的中点.
(I)求证:EF∥平面ADD
1A
1;
(Ⅱ)求二面角D-EF-A的余弦值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A
1B
1C
1D
1的棱长为1,E,F分别为D
1C
1,B
1C
1上的点.且满足
=λ,=λ(0<λ<1),
(1)若在AB上有一点P,使A
1C⊥平面PEF,求
的值.
(2)求此正方体在平面PEF内射影的面积.
查看答案和解析>>
科目:gzsx
来源:
题型:
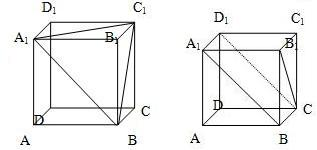
已知正方体ABCD-A
1B
1C
1D
1的棱长为a,
(1)用平面A
1BC
1截去一角后,求剩余部分的体积;
(2)求A
1B和B
1C所成的角.
查看答案和解析>>
科目:gzsx
来源:
题型:

已知正方体ABCD-A
1B
1C
1D
1的棱长为a.则直线CD与平面AB
1D
1所成的角的余弦值为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方体ABCD-A1B1C1D1的棱长为1,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
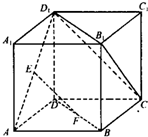
如图,已知正方体ABCD-A
1B
1C
1D
1的棱长为1,E、F分别为AD
1、BD的中点.
(1)求证:EF∥平面B
1D
1C;
(2)求二面角B
1-D
1C-A的大小;
(3)求三棱锥B
1-ACD
1的体积.
查看答案和解析>>

 如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,

 的概率P1;
的概率P1;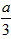 的概率P2。
的概率P2。
 如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F.G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的正投影.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F.G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的正投影. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是A1B1、CC1的中点,过D1、E、F作平面D1EGF交BB1于G.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是A1B1、CC1的中点,过D1、E、F作平面D1EGF交BB1于G. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.