科目:czsx
来源:
题型:阅读理解
阅读材料:
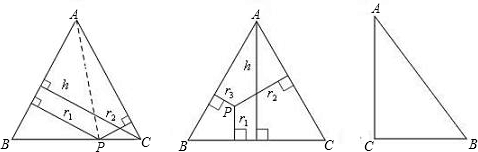
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:
AB•r1+AC•r2=AB•h,∴r
1+r
2=h(定值).
(1)类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(2)理解与应用
△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等?
(填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r=
.若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:
AB•r
1+
AC•r
2=
AC•h,∴r
1+r
2=h(定值).
(1)理解与应用:
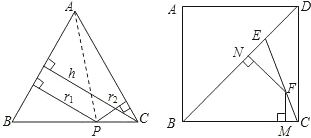
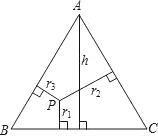
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
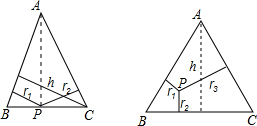
(2013•德城区二模)阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:
AB•r
1+
AC•r
2=
AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:
r1+r2+r3=.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
4
4
;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
查看答案和解析>>
科目:czsx
来源:2012届浙江省丽水市青田县中考模拟数学试卷(带解析)
题型:解答题
查看答案和解析>>
科目:czsx
来源:2011-2012学年浙江省丽水市青田县中考模拟数学试卷(解析版)
题型:解答题
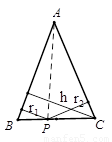
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两 腰的距离分别为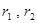 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则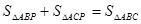 ,即:
,即: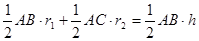 ,
,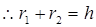 (1)理解与应用
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为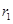 ,
,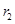 ,
,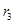 ,试证明:
,试证明: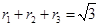 .
.
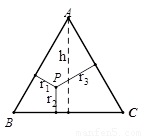
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为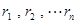 ,请问
,请问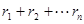 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
查看答案和解析>>
科目:czsx
来源:2012年湖北省咸宁市中考数学模拟试卷(八)(解析版)
题型:解答题
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AC•h,∴r
1+r
2=h(定值).
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.


查看答案和解析>>
科目:czsx
来源:2012年湖北省黄冈市浠水一中自主招生考试数学试卷(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:
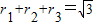
.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2010年河北省唐山市滦南县青坨营中学中考数学模拟试卷(解析版)
题型:解答题
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AC•h,∴r
1+r
2=h(定值).
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
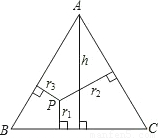
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2009年全国中考数学试题汇编《三角形》(11)(解析版)
题型:解答题
(2009•内江)阅读材料:
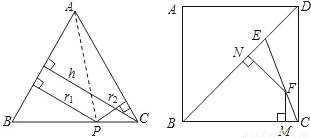
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AC•h,∴r
1+r
2=h(定值).
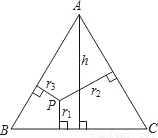
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.
查看答案和解析>>
科目:czsx
来源:2012年四川省广元市虎跳中学中考数学模拟试卷(七)(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:

.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即: ,∴r1+r2=h(定值).
,∴r1+r2=h(定值).
(1)类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).
(2)理解与应用
△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等?________(填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r=________.若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年浙江省丽水市青田二中中考数学模拟试卷(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:

.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2012年浙江省丽水市青田县中考数学模拟试卷(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:

.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2012年湖北省咸宁市温泉中学中考数学调研试卷(二)(解析版)
题型:解答题
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AC•h,∴r
1+r
2=h(定值).
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.


查看答案和解析>>
科目:czsx
来源:2012年浙江省金华市中考数学模拟试卷(一)(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:

.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2012年浙江省中考数学模拟试卷(六)(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:
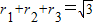
.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2013年浙江省中考数学模拟试卷(四)(解析版)
题型:解答题
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ABP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AB•h,∴r
1+r
2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,试证明:

.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于______;
(3)拓展与延伸
若边长为2的正n边形A
1A
2…An内部任意一点P到各边的距离为r
1,r
2,…r
n,请问r
1+r
2+…r
n是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.

查看答案和解析>>
科目:czsx
来源:2012年山东省德州市平原县中考数学一模试卷(解析版)
题型:解答题
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AC•h,∴r
1+r
2=h(定值).
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.


查看答案和解析>>
科目:czsx
来源:2013年四川省内江市全安中学中考数学一模试卷(解析版)
题型:解答题
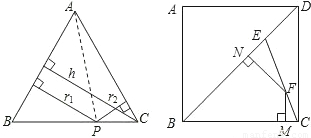
阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r
1,r
2,腰上的高为h,连接AP,则S
△ARP+S
△ACP=S
△ABC,即:

AB•r
1+

AC•r
2=

AC•h,∴r
1+r
2=h(定值).
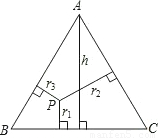
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为r
1,r
2,r
3,等边△ABC的高为h,试证明r
1+r
2+r
3=h(定值).
(3)拓展与延伸:
若正n边形A
1A
2…A
n,内部任意一点P到各边的距离为r
1r
2…r
n,请问r
1+r
2+…+r
n是否为定值?如果是,请合理猜测出这个定值.
查看答案和解析>>





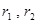 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则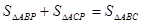 ,即:
,即: ,
, (1)理解与应用
(1)理解与应用 ,
, ,
,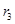 ,试证明:
,试证明: .
.

 ,请问
,请问 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。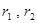 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则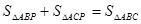 ,即:
,即: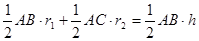 ,
,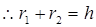 (1)理解与应用
(1)理解与应用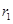 ,
,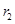 ,
,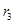 ,试证明:
,试证明: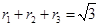 .
.
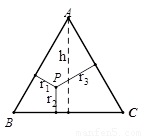
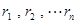 ,请问
,请问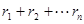 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h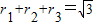 .
.
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h .
.
 ,∴r1+r2=h(定值).
,∴r1+r2=h(定值).
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h .
.
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h .
.
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).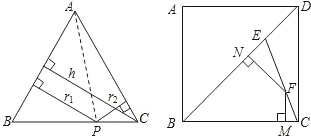

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h .
.
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h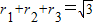 .
.
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AB•h,∴r1+r2=h
AB•h,∴r1+r2=h .
.
 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).
