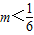科目:czsx
来源:
题型:
已知抛物线y=x
2-(4m+1)x+2m-1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,
-)的下方,那么m的取值范围是( )
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x
2+(m-4)x+2m+4与x轴交于点A(x
1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D.
(1)求C、D两点坐标.
(2)求过点B、C、D三点的抛物线的解析式.
(3)若P是(2)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且S
△ABH=24S
△BDP,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0)、B(x2,0)两点,与y轴交于点C,且x1<x2,x1+2x2=0.若点A关于y轴的对称点是点D.
(1)求过点C、B、D的抛物线的解析式;
(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△HBD与△CBD的面积相等,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=x
2+(m-2)x-2m,当m
=±2
=±2
时,顶点在坐标轴上.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x
2+(m-4)x+2m+4与x轴相交于A(x
1,0),B(x
2,0)与y轴交于点C,且x
1=-2x
2(x
1<x
2),点A关于y轴的对称点为D.
(1)确定A,B,C三点的坐标;
(2)求过B,C,D三点的抛物线的解析式;
(3)若y=3与(2)小题中所求抛物线交于M,N,以MN为一边,抛物线上任一点P(x,y)为顶点作为平行四边形,若平行四边形面积为S,写出S与P点纵坐标y的函数关系式;
(4)当
<x<4时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•沙市区一模)如图,已知抛物线y=x
2-(m
2-2)x-2m与x轴交与点A(x
1,0),B(x
2,0),与y轴交与点C,且满足
+=.
(1)求这条抛物线的解析式;
(2)若点M是这条抛物线对称轴上的一个动点,当MB+MC的值最小时,求点M的坐标.
查看答案和解析>>
科目:czsx
来源:重庆
题型:解答题
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0)、B(x2,0)两点,与y轴交于点C,且x1<x2,x1+2x2=0.若点A关于y轴的对称点是点D.
(1)求过点C、B、D的抛物线的解析式;
(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△HBD与△CBD的面积相等,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知抛物线y=x2-(m2-2)x-2m与x轴交与点A(x1,0),B(x2,0),与y轴交与点C,且满足
如图,已知抛物线y=x2-(m2-2)x-2m与x轴交与点A(x1,0),B(x2,0),与y轴交与点C,且满足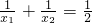 .
.
(1)求这条抛物线的解析式;
(2)若点M是这条抛物线对称轴上的一个动点,当MB+MC的值最小时,求点M的坐标.
查看答案和解析>>
科目:czsx
来源:2003年重庆市中考数学试卷(解析版)
题型:解答题
(2003•重庆)已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0)、B(x2,0)两点,与y轴交于点C,且x1<x2,x1+2x2=0.若点A关于y轴的对称点是点D.
(1)求过点C、B、D的抛物线的解析式;
(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△HBD与△CBD的面积相等,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版)
题型:解答题
(2004•乌鲁木齐)已知抛物线y=-x
2+(m-4)x+2m+4与x轴相交于A(x
1,0),B(x
2,0)与y轴交于点C,且x
1=-2x
2(x
1<x
2),点A关于y轴的对称点为D.
(1)确定A,B,C三点的坐标;
(2)求过B,C,D三点的抛物线的解析式;
(3)若y=3与(2)小题中所求抛物线交于M,N,以MN为一边,抛物线上任一点P(x,y)为顶点作为平行四边形,若平行四边形面积为S,写出S与P点纵坐标y的函数关系式;
(4)当
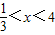
时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013年湖北省荆州市沙市区中考数学一模试卷(解析版)
题型:解答题
如图,已知抛物线y=x
2-(m
2-2)x-2m与x轴交与点A(x
1,0),B(x
2,0),与y轴交与点C,且满足
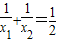
.
(1)求这条抛物线的解析式;
(2)若点M是这条抛物线对称轴上的一个动点,当MB+MC的值最小时,求点M的坐标.

查看答案和解析>>
科目:czsx
来源:重庆市模拟题
题型:解答题
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2 ,0)两点,与y轴交于点C, 若点A关于y轴对称点是点D。
(1)求C、D两点坐标。
(2)求过点B、C、D三点的抛物线的解析式。
(3)若P是(2)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且S△ABH=24S△BDP,求直线PH的解析式。
查看答案和解析>>
科目:czsx
来源:2004年新疆乌鲁木齐市中考数学试卷(解析版)
题型:解答题
(2004•乌鲁木齐)已知抛物线y=-x
2+(m-4)x+2m+4与x轴相交于A(x
1,0),B(x
2,0)与y轴交于点C,且x
1=-2x
2(x
1<x
2),点A关于y轴的对称点为D.
(1)确定A,B,C三点的坐标;
(2)求过B,C,D三点的抛物线的解析式;
(3)若y=3与(2)小题中所求抛物线交于M,N,以MN为一边,抛物线上任一点P(x,y)为顶点作为平行四边形,若平行四边形面积为S,写出S与P点纵坐标y的函数关系式;
(4)当

时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
查看答案和解析>>
科目:czsx
来源:2003年全国中考数学试题汇编《二次函数》(03)(解析版)
题型:解答题
(2003•重庆)已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0)、B(x2,0)两点,与y轴交于点C,且x1<x2,x1+2x2=0.若点A关于y轴的对称点是点D.
(1)求过点C、B、D的抛物线的解析式;
(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△HBD与△CBD的面积相等,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:2005年浙江省杭州市萧山区中考数学二模试卷(解析版)
题型:解答题
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0)、B(x2,0)两点,与y轴交于点C,且x1<x2,x1+2x2=0.若点A关于y轴的对称点是点D.
(1)求过点C、B、D的抛物线的解析式;
(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△HBD与△CBD的面积相等,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D.
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D.
(1)求C、D两点坐标.
(2)求过点B、C、D三点的抛物线的解析式.
(3)若P是(2)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且S△ABH=24S△BDP,求直线PH的解析式.
查看答案和解析>>
科目:czsx
来源:同步题
题型:解答题
已知抛物线y=x2+ (m-2)x-2m。
(1)当顶点在y 轴上时,求m 的值;
(2)若m=-2,写出抛物线的对称轴和顶点坐标;
(3)若抛物线经过原点,求m 的值。
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》好题集(10):2.8 二次函数与一元二次方程(解析版)
题型:选择题
已知抛物线y=x
2-(4m+1)x+2m-1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,

)的下方,那么m的取值范围是( )
A.
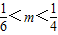
B.

C.

D.全体实数
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》好题集(06):6.3 二次函数与一元二次方程(解析版)
题型:选择题
已知抛物线y=x
2-(4m+1)x+2m-1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,
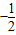
)的下方,那么m的取值范围是( )
A.

B.
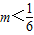
C.

D.全体实数
查看答案和解析>>
科目:czsx
来源:不详
题型:单选题
已知抛物线y=x
2-(4m+1)x+2m-1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,
-)的下方,那么m的取值范围是( )
查看答案和解析>>

 已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D.
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D. (2013•沙市区一模)如图,已知抛物线y=x2-(m2-2)x-2m与x轴交与点A(x1,0),B(x2,0),与y轴交与点C,且满足
(2013•沙市区一模)如图,已知抛物线y=x2-(m2-2)x-2m与x轴交与点A(x1,0),B(x2,0),与y轴交与点C,且满足 如图,已知抛物线y=x2-(m2-2)x-2m与x轴交与点A(x1,0),B(x2,0),与y轴交与点C,且满足
如图,已知抛物线y=x2-(m2-2)x-2m与x轴交与点A(x1,0),B(x2,0),与y轴交与点C,且满足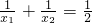 .
.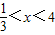 时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.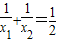 .
.
 时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由. 已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D.
已知抛物线y=-x2+(m-4)x+2m+4与x轴交于点A(x1,0),B(2,0)两点,与y轴交于点C.若点A关于y轴对称点是点D. )的下方,那么m的取值范围是( )
)的下方,那么m的取值范围是( )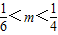


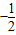 )的下方,那么m的取值范围是( )
)的下方,那么m的取值范围是( )