
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
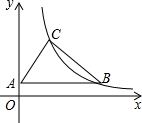 如图,Rt△ABC 中,∠C=90°,AC=6,BC=8,点A在y轴上,B,C在反比例函数y=
如图,Rt△ABC 中,∠C=90°,AC=6,BC=8,点A在y轴上,B,C在反比例函数y=| k |
| x |
科目:czsx 来源: 题型:
| 2 |
| 2 |
科目:czsx 来源: 题型:
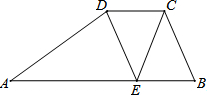 (2013•房山区二模)如图,四边形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.若CE=CB,且tan∠B=3,求四边形ABCD的面积.
(2013•房山区二模)如图,四边形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.若CE=CB,且tan∠B=3,求四边形ABCD的面积.科目:czsx 来源: 题型:
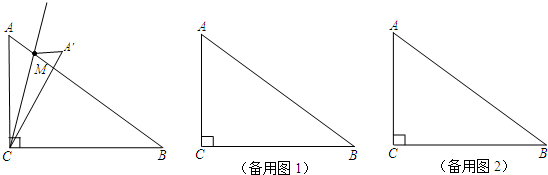
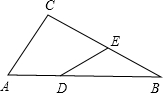 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是科目:czsx 来源:2012届江苏省泰州市海陵区九年级二模数学卷(带解析) 题型:解答题
如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.(1)求证:AE=AC(2)若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.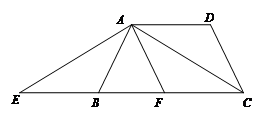
科目:czsx 来源: 题型:
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是________________.

科目:czsx 来源:2010-2011学年北京市考一模数学试卷 题型:填空题
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是________________.

科目:czsx 来源:2011届北京市怀柔区中考一模数学试卷 题型:填空题
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是________________.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:

科目:czsx 来源:中考数学专项练习 题型:044
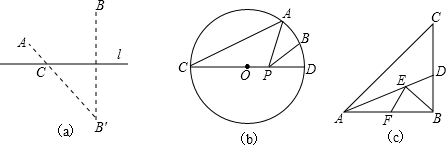
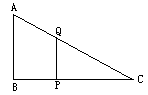
已知:如图,Rt△ABC中,∠B=![]() ,AB=c,BC=a,动点P在BC上移动,QP⊥BC交AC于Q,设PQ的长为y,BP的长为x.写出y与x之间函数关系式,并求出自变量x的取值范围.
,AB=c,BC=a,动点P在BC上移动,QP⊥BC交AC于Q,设PQ的长为y,BP的长为x.写出y与x之间函数关系式,并求出自变量x的取值范围.
科目:czsx 来源: 题型:解答题
 如图,四边形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.若CE=CB,且tan∠B=3,求四边形ABCD的面积.
如图,四边形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.若CE=CB,且tan∠B=3,求四边形ABCD的面积.科目:czsx 来源:2011-2012学年江苏省泰州市海陵区九年级二模数学卷(解析版) 题型:解答题
如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.(1)求证:AE=AC(2)若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.

【解析】根据平行四边形的性质和菱形的性质求证
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.(1)求证:AE=AC(2)若AB⊥AC,F是BC的中点,试判断四边形AFCD的形状,并说明理由.

【解析】根据平行四边形的性质和菱形的性质求证
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2013年北京市房山区中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源:湖北省月考题 题型:填空题

科目:czsx 来源: 题型:填空题
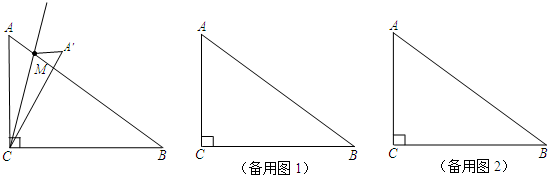
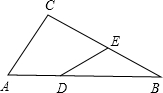 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是________.
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是________.