科目:czsx 来源: 题型:解答题
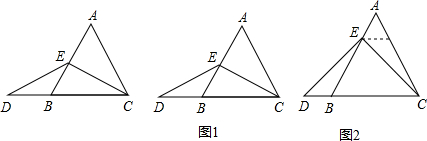
 如图,C为线段AB的中点,点D在线段CB上.
如图,C为线段AB的中点,点D在线段CB上.科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题
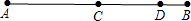
科目:czsx 来源: 题型:
 如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2.一动点P从C出发,沿CB方向在线段BC上作匀速运动.
如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2.一动点P从C出发,沿CB方向在线段BC上作匀速运动.科目:czsx 来源: 题型:
如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2。一动点P从C出发,沿CB方向在线段BC上作匀速运动。
(1)若三角形ABP的面积S关于运动时间t的函数图象如图②所示,则可得BC长为 ; ;(4分。)
(2)在(1)的条件下,试求∠B的度数。(4分。)


图① 图②
科目:czsx 来源: 题型:

科目:czsx 来源:2011-2012学年江苏省吕良中学八年级第一学期第二次阶段检测数学卷.doc 题型:解答题
如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2。一动点P从C出发,沿CB方向在线段BC上作匀速运动。
(1)若三角形ABP的面积S关于运动时间t的函数图象如图②所示,则可得BC长为 ; ;(4分。)
(2)在(1)的条件下,试求∠B的度数。(4分。)

图① 图②
科目:czsx 来源:2013届江苏省八年级第一学期第二次阶段检测数学卷 题型:选择题
如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2。一动点P从C出发,沿CB方向在线段BC上作匀速运动。
(1)若三角形ABP的面积S关于运动时间t的函数图象如图②所示,则可得BC长为 ; ;(4分。)
(2)在(1)的条件下,试求∠B的度数。(4分。)


图① 图②
科目:czsx 来源:2014年初中毕业升学考试(黑龙江牡丹江卷)数学(解析版) 题型:解答题
如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
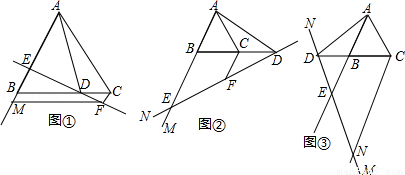
(1)当点D在线段BC上,∠NDB为锐角时,如图①,求证:CF+BE=CD;
(提示:过点F作FM∥BC交射线AB于点M.)
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;当点D在线段CB的延长线上,∠NDB为钝角时,如图③,请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
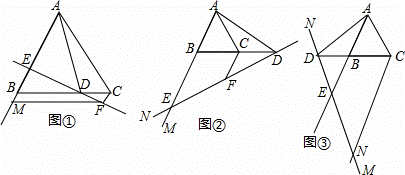
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4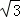 ,则BE= ,CD= .
,则BE= ,CD= .
科目:czsx 来源: 题型:解答题
 如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2.一动点P从C出发,沿CB方向在线段BC上作匀速运动.
如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2.一动点P从C出发,沿CB方向在线段BC上作匀速运动.科目:czsx 来源:不详 题型:解答题


科目:czsx 来源: 题型:

| 3 |
科目:czsx 来源: 题型:
如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
(1)当点D在线段BC上,∠NDB为锐角时,如图①,求证:CF+BE=CD;
(提示:过点F作FM∥BC交射线AB于点M.)
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;当点D在线段CB的延长线上,∠NDB为钝角时,如图③,请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4 ,则BE= 8 ,CD= 4或8 .
,则BE= 8 ,CD= 4或8 .
科目:czsx 来源:2015-2016学年河北省保定市竞秀区八年级下期末数学试卷(解析版) 题型:解答题
如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
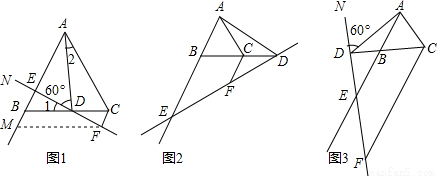
(1)当点D在线段BC上,∠NDB为锐角时,如图①,
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;
当点D在线段CB的延长线上,∠NDB为钝角时,如图③;
请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4 ,直接写出BE和CD的长度.
,直接写出BE和CD的长度.
科目:czsx 来源:2013年河南省许昌市中考数学一模试卷(解析版) 题型:解答题
 .点D在CB的延长线上,且ED=EC,求CD的长.
.点D在CB的延长线上,且ED=EC,求CD的长.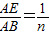 (n>0),△ABC边长为m,则CD的长为______(用含n,m的代数式表示)试写出解答过程.
(n>0),△ABC边长为m,则CD的长为______(用含n,m的代数式表示)试写出解答过程.
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
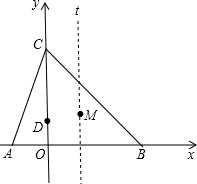 如图,平面直线坐标中,A(-1,0),点C为y轴正半轴上一点,且AC=
如图,平面直线坐标中,A(-1,0),点C为y轴正半轴上一点,且AC=| 10 |
| 2 |
科目:czsx 来源:2016年初中毕业升学考试(四川达州卷)数学(解析版) 题型:判断题
△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为 ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
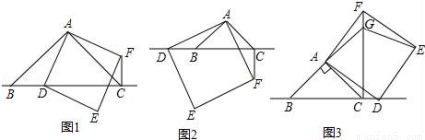
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ,CD=
,CD= BC,请求出GE的长.
BC,请求出GE的长.
科目:czsx 来源: 题型: