科目:czsx
来源:
题型:
如图,数轴原点为O,A、B是数轴上的两点,点A对应的数是1,点B对应的数是-4,动点P、Q同时从A、B出发,分别以1个单位/秒和3个单位/秒的速度沿着数轴正方向运动,设运动时间为t秒 (t>0).

(1)AB两点间的距离是
;
动点P对应的数是
;(用含t的代数式表示)
动点Q对应的数是
;(用含t的代数式表示)
(2)几秒后,点O恰好为线段PQ中点?
(3)几秒后,恰好有OP:OQ=1:2?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,有一数轴原点为O,点A所对应的数是-1
,点A沿数轴匀速平移经过原点到达点B.
(1)如果OA=OB,那么点B所对应的数是什么?
(2)从点A到达点B所用时间是3秒,求该点的运动速度.
(3)从点A沿数轴匀速平移经过点K到达点C,所用时间是9秒,且KC=KA,分别求点K和点C所对应的数.
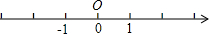
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,有一数轴原点为O,点A所对应的数是-1 ,点A沿数轴匀速平移经过原点到达点B.
,点A沿数轴匀速平移经过原点到达点B.
(1)如果OA=OB,那么点B所对应的数是什么?
(2)从点A到达点B所用时间是3秒,求该点的运动速度.
(3)从点A沿数轴匀速平移经过点K到达点C,所用时间是9秒,且KC=KA,分别求点K和点C所对应的数.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,过原点的直线l
1:y=3x,l
2:y=
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
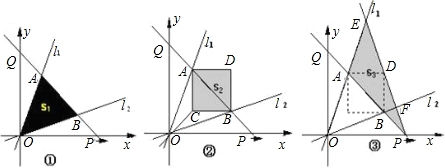
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)
(1)S
l关于t的函数解析式为
;(2)直线OC的函数解析式为
;
(3)S
2关于t的函数解析式为
;(4)S
3关于t的函数解析式为
.
查看答案和解析>>
科目:gzsx
来源:
题型:

如图,过原点O的直线与函数y=3
x的图象交于A,B两点,过B作y轴的垂线交函数y=9
x的图象于点C,若AC恰好平行于y轴,则点A的坐标为
(log32,2)
(log32,2)
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
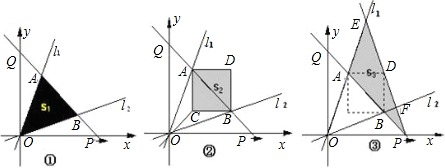
如图,过原点的直线l1:y=3x,l2:y= x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
(1)Sl关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S2关于t的函数解析式为______;(4)S3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(51):34.4 二次函数的应用(解析版)
题型:解答题
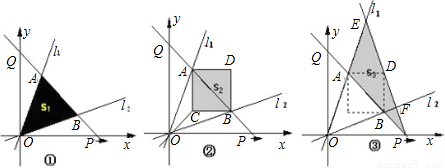
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)
(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)

(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(49):27.3 实践与探索(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)
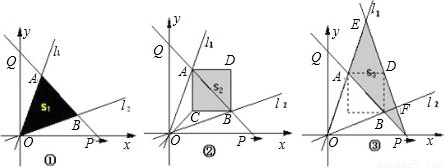
(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(47):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)

(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(51):2.8 二次函数的应用(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)

(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(47):20.5 二次函数的一些应用(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)

(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(47):2.4 二次函数的应用(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)

(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(47):23.5 二次函数的应用(解析版)
题型:解答题
如图,过原点的直线l
1:y=3x,l
2:y=

x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l
1、l
2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为S
l(如图①).以AB为对角线作正方形ACBD,其面积为S
2(如图②).连接PD并延长,交l
1于点E,交l
2于点F.设△PEA的面积为S
3;(如图③)
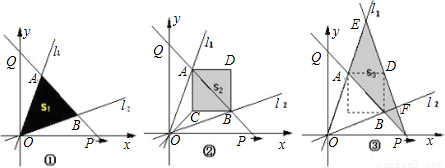
(1)S
l关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S
2关于t的函数解析式为______;(4)S
3关于t的函数解析式为______.
查看答案和解析>>
科目:gzsx
来源:2010年江苏省高一第一学期期末测试数学试卷
题型:填空题
如图,过原点O的直线与函数y=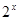 的图像交与A、B两点,
的图像交与A、B两点,
过B作y轴的垂线交函数y= 的图像于点C,若AC平行于y轴,
的图像于点C,若AC平行于y轴,
则点A的坐标为 ▲ .
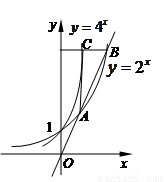
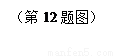
查看答案和解析>>
科目:gzsx
来源:
题型:
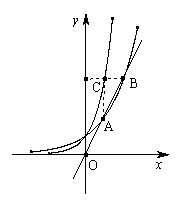
如图,过原点O的直线与函数y= 的图像交与A、B两点,过B作y轴的垂线交函数y=
的图像交与A、B两点,过B作y轴的垂线交函数y= 的图像于点C,若AC平行于y轴,则点A的坐标为__________.
的图像于点C,若AC平行于y轴,则点A的坐标为__________.
查看答案和解析>>
科目:gzsx
来源:
题型:
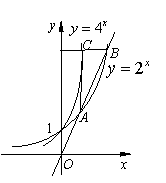
如图,过原点O的直线与函数y= 的图像交与A、B两点,过B作y轴的垂线交函数y=
的图像交与A、B两点,过B作y轴的垂线交函数y= 的图像于点C,若AC平行于y轴,则点A的坐标为 ▲ .
的图像于点C,若AC平行于y轴,则点A的坐标为 ▲ .
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,过原点O的直线与函数y=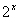 的图像交与A、B两点,过B作y轴的垂线交函数y=
的图像交与A、B两点,过B作y轴的垂线交函数y= 的图像于点C,若AC平行于y轴,则点A的坐标为__________.
的图像于点C,若AC平行于y轴,则点A的坐标为__________.

查看答案和解析>>
科目:czsx
来源:
题型:
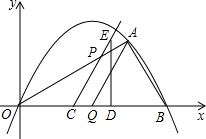
如图经过原点的抛物线y=ax
2+bx经过点A、B两点,其中OB=12,且
∠OAB=90°,∠AOB=30°,点Q是OB的中点,连结AQ.一动点C从Q点出发,以每秒1个单位长度的速度沿线段QO匀速运动,到达O点后,立即以原速度沿线段OQ返回;另一动点D从Q点出发,以每秒1个单位长度的速度沿射线QB匀速运动,点C、D同时出发,当点C返回到点Q时停止运动,在点C、D的运动过程中,过点C作直线CE∥AQ,过点D作DE⊥x轴交CE于点E.设运动的时间为t秒(t>0).
(1)求出该抛物线的函数解析式.
(2)求当t为何值时,点E在抛物线上,
(3)在点C从点O返回到点Q的过程中,直接写出以P、B、D、E组成的四边形面积的最小值.
(4)设射线CE与线段OA的交点为P,是否存在这样的t,使△POQ是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,过原点的直线与反比例函数y=
(x>0)、反比例函数y=
(x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=
(x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为
.
查看答案和解析>>


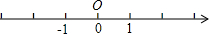
 ,点A沿数轴匀速平移经过原点到达点B.
,点A沿数轴匀速平移经过原点到达点B.

 如图,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC恰好平行于y轴,则点A的坐标为
如图,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC恰好平行于y轴,则点A的坐标为 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
 的图像交与A、B两点,
的图像交与A、B两点, 的图像于点C,若AC平行于y轴,
的图像于点C,若AC平行于y轴,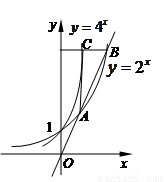
 如图经过原点的抛物线y=ax2+bx经过点A、B两点,其中OB=12,且
如图经过原点的抛物线y=ax2+bx经过点A、B两点,其中OB=12,且 如图,过原点的直线与反比例函数y=
如图,过原点的直线与反比例函数y=