
科目:gzsx 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
科目:gzsx 来源:2012年天津市河西区高考数学一模试卷(理科)(解析版) 题型:选择题
 +
+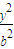 =1的离心率为e1,双曲线
=1的离心率为e1,双曲线 -
- =1的离心率为e2,抛物线y2=2px的离心率为e3,a=5
=1的离心率为e2,抛物线y2=2px的离心率为e3,a=5 ,b=(
,b=( )
) ,c=5
,c=5 ,则a,b,c之间的大小关系是( )
,则a,b,c之间的大小关系是( )科目:gzsx 来源:2005-2006学年江苏省苏州市吴中区高二(上)期末数学试卷(解析版) 题型:选择题
 (a>b>0)的离心率为e1,准线为l1、l2;双曲线
(a>b>0)的离心率为e1,准线为l1、l2;双曲线 离心率为e2,准线为l3、l4;若l1、l2、l3、l4正好围成一个正方形,则
离心率为e2,准线为l3、l4;若l1、l2、l3、l4正好围成一个正方形,则 等于( )
等于( )



科目:gzsx 来源: 题型:

(1)求Q点的轨迹方程;
(2)设(1)中所求轨迹为C2,C1、C2的离心率分别为e1、e2,当e1≥![]() 时,求e2的取值范围.
时,求e2的取值范围.
科目:gzsx 来源: 题型:
| x2 |
| 4 |
3
| ||
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
科目:gzsx 来源:2012-2013学年福建省三明九中高二(上)第二次月考数学试卷(美术班)(解析版) 题型:填空题
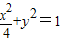 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为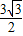 ;
;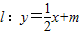 与椭圆有两个交点,求m的取值范围.
与椭圆有两个交点,求m的取值范围. 科目:gzsx 来源:不详 题型:解答题
| x2 |
| 4 |
3
| ||
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| e12 |
| 1 |
| e22 |
科目:gzsx 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ③④ |
科目:gzsx 来源: 题型:
| x2 |
| 36 |
| y2 |
| 49 |
| 7 |
| 3 |
科目:gzsx 来源:不详 题型:解答题
| x2 |
| 36 |
| y2 |
| 49 |
| 7 |
| 3 |
科目:gzsx 来源:课标综合版 专题复习 题型:
| |||||
科目:gzsx 来源: 题型:
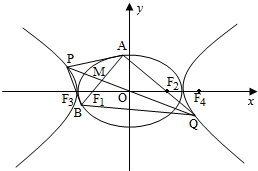 如图,O为坐标原点,椭圆C1:
如图,O为坐标原点,椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
科目:gzsx 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
科目:gzsx 来源: 题型:单选题
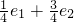 =1
=1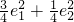 =1
=1 =1
=1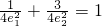
科目:gzsx 来源:2011年浙江省杭州市萧山区高考数学模拟试卷10(理科)(解析版) 题型:选择题
 =1
=1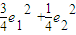 =1
=1 =1
=1
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| BP |
| AQ |
| BQ |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| OQ |