练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >如图.已知抛物线y=-x2 mx 3与x轴交于A.B两点

    如图.已知抛物线y=-x2 mx 3与x轴交于A.B两点答案解析

    科目：czsx 来源： 题型：

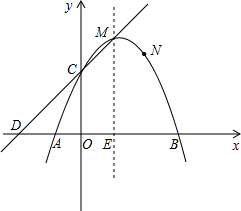    如图，已知抛物线的顶点坐标为M（1，4），且经过点N（2，3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C．
    （1）求抛物线的解析式及点A、B、C的坐标；
    （2）若直线y=kx+t经过C、M两点，且与x轴交于点D，探索并判断四边形CDAN是怎样的四边形？并对你得到的结论予以证明；
    （3）直线y=mx+2与抛物线交于T，Q两点．是否存在这样的实数m，使以线段TQ为直径的圆恰好过坐标原点？若存在，请求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：四川省模拟题 题型：解答题

    如图，已知抛物线的顶点坐标为M（1，4），且经过点N（2，3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C。
    （1）求抛物线的解析式及点A、B、C的坐标；
    （2）若直线y=kx+t经过C、M两点，且与x轴交于点D，探索并判断四边形CDAN是怎样的四边形？并对你得到的结论予以证明；
    （3）直线y=mx+2与抛物线交于T，Q两点，是否存在这样的实数m，使以线段TQ为直径的圆恰好过坐标原点，若存在，请求出m的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：czsx 来源：2012年福建省漳州市中考数学模拟试卷（二）（解析版） 题型：解答题

    如图，已知抛物线的顶点坐标为M（1，4），且经过点N（2，3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C．
    （1）求抛物线的解析式及点A、B、C的坐标；
    （2）若直线y=kx+t经过C、M两点，且与x轴交于点D，探索并判断四边形CDAN是怎样的四边形？并对你得到的结论予以证明；
    （3）直线y=mx+2与抛物线交于T，Q两点．是否存在这样的实数m，使以线段TQ为直径的圆恰好过坐标原点？若存在，请求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：


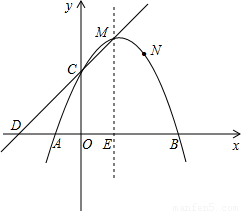
    如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B。

    （1）若直线y＝mx＋n经过B、C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴x＝－1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

    （3）设点P为抛物线的对称轴x＝－1上的一个动点，求使△BPC为直角三角形的点P的坐标。

    查看答案和解析>>

    科目：czsx 来源：2016届山东省滨州市中考一模数学试卷（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

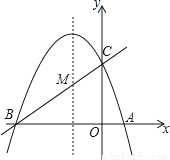
    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

    （3）设点P为抛物线的对称轴x=-1上的一个动点，求使△BPC为直角三角形的点P的坐标．

    查看答案和解析>>

    科目：czsx 来源：2016届广东省汕头市龙湖区九年级下学期中考数学模拟试卷（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标．

    查看答案和解析>>

    科目：czsx 来源：2016届山东聊城莘县九年级下期第二次模拟测试数学试卷（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

    （3）设点P为抛物线的对称轴x=-1上的一个动点，求使△BPC为直角三角形的点P的坐标．

    查看答案和解析>>

    科目：czsx 来源：2016届山东德州陵城区九年级下期二模考试数学试卷（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

    （3）设点P为抛物线的对称轴x=-1上的一个动点，求使△BPC为直角三角形的点P的坐标．

    查看答案和解析>>

    科目：czsx 来源：2015-2016学年江苏省南通市海门市八年级（下）期末数学试卷（解析版） 题型：计算题

    如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

    （3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．

    查看答案和解析>>

    科目：czsx 来源：2016-2017学年山东济宁兖州区九年级上期中数学试卷（解析版） 题型：解答题

    如图，已知抛物线y=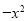+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），

    （1）求m的值及抛物线的顶点坐标．

    （2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    19．如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
    （2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    12．如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
    （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
    （2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标．
    （3）在抛物线的对称轴上是否存在一点P，使△BPC为直角三角形？若存在，请求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

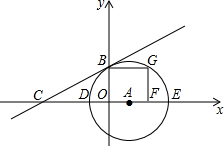    如图，已知直线l：y=kx+b（k，b为常数，且k≠0）与x轴，y轴分别交于点C，B两点．⊙A的圆心在x轴上，与x轴交于D，E两点，且与直线l相切于点B．作矩形OBGF，使得点G在⊙A上，F在x轴上．
    （1）填空：用k，b表示点的坐标：C
     
    ；B
     
    ；A
     
    ； 
    （2）当矩形OBGF是正方形时，求k的值； 
    （3）在（2）的前提下，有一条抛物线y=ax2+mx+c（a，m，c均为常数，其中a≠0），经过点D，E两点，且顶点H，在弓形BG内（包括边界
    BG
    和弦BG），当
    		5
    ≤b≤5，请你求出a的范围．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    19．如图1，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+bx+c（a≠0）的顶点为（-3，$\frac{25}{4}$），与x轴交于A，B两点（点A在点B的右侧）与y轴交于点C，D为BO的中点，直线DC解析式为y=kx+4（k≠0）
    （1）求抛物线的解析式和直线CD的解析式．
    （2）点P是抛物线第二象限部分上使得△PDC面积最大的一点，点E为DO的中点，F是线段DC上任意一点（不含端点）．连接EF，一动点M从点E出发沿线段EF以每秒1个单位长度的速度运动到F点，再沿线段FC以每秒$\sqrt{2}$个单位长度的速度运动到C点停止．当点M在整个运动中同时最少为t秒时，求线段PF的长及t值．
    （3）如图2，直线DN：y=mx+2（m≠0）经过点D，交y轴于点N，点R是已知抛物线上一动点，过点R作直线DN的垂线RH，垂足为H，直线RH交x轴与点Q，当∠DRH=∠ACO时，求点Q的坐标．

    查看答案和解析>>