Question

19．如图1，在平面直角坐标系中，O为坐标原点，抛物线y=ax²+bx+c（a≠0）的顶点为（-3，$\frac{25}{4}$），与x轴交于A，B两点（点A在点B的右侧）与y轴交于点C，D为BO的中点，直线DC解析式为y=kx+4（k≠0）
（1）求抛物线的解析式和直线CD的解析式．
（2）点P是抛物线第二象限部分上使得△PDC面积最大的一点，点E为DO的中点，F是线段DC上任意一点（不含端点）．连接EF，一动点M从点E出发沿线段EF以每秒1个单位长度的速度运动到F点，再沿线段FC以每秒$\sqrt{2}$个单位长度的速度运动到C点停止．当点M在整个运动中同时最少为t秒时，求线段PF的长及t值．
（3）如图2，直线DN：y=mx+2（m≠0）经过点D，交y轴于点N，点R是已知抛物线上一动点，过点R作直线DN的垂线RH，垂足为H，直线RH交x轴与点Q，当∠DRH=∠ACO时，求点Q的坐标．

Answer 1

分析 （1）设抛物线解析式y=a（x+3）²+$\frac{25}{4}$，把点C（0，4）代入即可求出a，再令y=0，求出点B以及点D坐标即可解决问题．
（2）如图1中，过点C作y轴的垂线，过点E作x轴的垂线两线交于点M，EM与CD交于点F，此时点F就是所求的点，时间最短，再利用三角形面积公式求出使得△PCD面积最大的点P坐标，即可求出PF的长．
（3）分两种情形，①如图2中，当∠DR₁H₁=∠DR₂H₂=∠ACO时，利用勾股定理求出点M的坐标，求出直线DM，解方程组求出R₁，R₂坐标，再求出直线R₁H₁，R₂H₂即可解决问题，②当∠DR₃H₃=∠ACO时，求出R₃坐标后求出直线R₃H₃即可解决问题．

解答 解：（1）由题意抛物线顶点（-3，$\frac{25}{4}$），点C坐标（0，4），
设抛物线解析式y=a（x+3）²+$\frac{25}{4}$，把点C（0，4）代入得a=-$\frac{1}{4}$，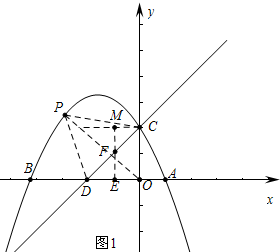
所以抛物线为y=-$\frac{1}{4}$（x+3）²+$\frac{25}{4}$=-$\frac{1}{4}$x²-$\frac{3}{2}$x+4，
令y=0，得x²+6x-16=0，x=-8或2，所以点B（-8，0），点A（2，0），D（-4，0）
把点D（-4，0）代入y=kx+4中得k=1，所以直线CD解析式为y=x+4．
（2）如图1中，过点C作y轴的垂线，过点E作x轴的垂线两线交于点M，EM与CD交于点F，
此时点F就是所求的点，时间最短．
∵OC=OD=4，
∴∠DCO=45°，
∴∠MCF=90°-∠DCO=45°，
∵∠MCO=∠MEO=∠EOC=90°，
∴四边形MEOC是矩形，
∴∠EMC=90°，
∴∠MFC=∠MCF=45°，
∴FC=$\sqrt{2}$FM，
∵t=EF+$\frac{CF}{\sqrt{2}}$=EF+FM，
∴EM⊥CM时，时间最短，
∴t=4秒．
设点P（m，-$\frac{1}{4}{m}^{2}$-$\frac{3}{2}$m+4），
∵S_△PCD=S_△PDO+S_△PCO-S_△DCO=$\frac{1}{2}$×$4×（-\frac{1}{4}{m}^{2}-\frac{3}{2}m+4）+\frac{1}{2}×4×（-m）$-8=-$\frac{1}{2}$m²-5m，
∴m=-5时，△PCD面积最大，此时P（-5，$\frac{21}{4}$），∵点F（-2，2），
∴PF=$\sqrt{（-5+2）^{2}+（\frac{21}{4}-2）^{2}}$=$\frac{\sqrt{313}}{4}$，
（3）如图2中，①当∠DR₁H₁=∠DR₂H₂=∠ACO，
∵点N（0，2），D（-4，0），C（0，4），A（2，0），
∴直线DN为y=$\frac{1}{2}$x+2，直线AC为y=-2x+4，
∴K₁K₂=-1，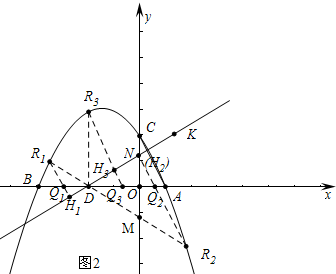
∴AC⊥DN，
∴∠ACO=∠ODN，
∴∠DNO=∠OAC，
∵∠DR₁H₁=∠DR₂H₂=∠ACO，
∴∠MDN=∠MND，
∴MN=DM，设OM=m，则（m+2）²=m²+4²解得m=3，
∴点M（0，-3），直线DM为y=-$\frac{3}{4}$x-3，
由$\left\{\begin{array}{l}{y=-\frac{3}{4}x-3}\\{y=-\frac{1}{4}{x}^{2}-\frac{3}{2}x+4}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-7}\\{y=\frac{9}{4}}\end{array}\right.或\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$，
∴R₁（-7，$\frac{9}{4}$），R₂（4，-6），
∴直线R₁H₁为y=-2x-$\frac{47}{4}$，此时Q₁（-$\frac{47}{8}$，0），
直线R₂H₂为y=-2x+2，此时Q₂（1，0），
②当∠DR₃H₃=∠ACO时，∵R₃Q₃⊥DC，AC⊥DC，
∴∠R₃DH₃=∠CNK，
∴DR₃∥OC，
∴R₃（-4，6），直线R₃Q₃为y=-2x-2，
∴Q₃（-1，0）．
综上所述满足条件的点Q的坐标为Q₁（-$\frac{47}{8}$，0），Q₂（1，0），Q₃（-1，0）．

点评 本题考查待定系数法确定函数解析式、勾股定理、两条直线平行或垂直时的k的关系，解题时体现了转化的思想，用方程或一次函数解决问题是解题的关键，综合性强，计算量大，属于中考压轴题．