
科目:czsx 来源:2013-2014学年四川省内江市九年级第一学期期末考试数学试卷(解析版) 题型:解答题
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).

(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使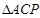 与
与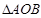 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
科目:czsx 来源:2013-2014学年黑龙江伊春区九年级上学期期末检测数学试卷(解析版) 题型:解答题
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D.
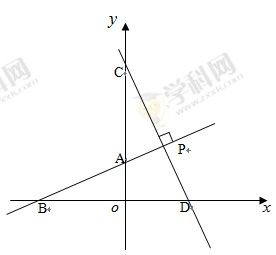
(1)求出点A、点B的坐标.
(2)请求出直线CD的解析式.
(3)若点M为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B、P、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使 与
与 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D.
(1)求出点A、点B的坐标.
(2)请求出直线CD的解析式.
(3)若点M为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B、P、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
科目:czsx 来源:不详 题型:解答题

 与
与 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.科目:czsx 来源:不详 题型:解答题

科目:gzsx 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练12练习卷(解析版) 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
科目:gzsx 来源: 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC=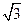 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.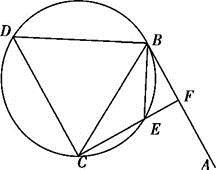
科目:gzsx 来源: 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.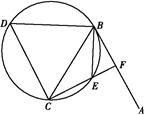
(1)证明:DB=DC;
(2)设圆的半径为1,BC=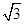 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
科目:gzsx 来源:2014高考名师推荐数学理科几何证明选讲(解析版) 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.

科目:gzsx 来源:不详 题型:解答题
 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
科目:gzsx 来源: 题型:
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
科目:czsx 来源: 题型:
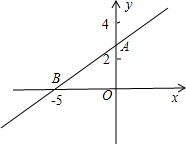 如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).科目:czsx 来源: 题型:
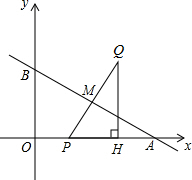 如图直线y=-
如图直线y=-| 1 | 2 |
科目:czsx 来源: 题型:
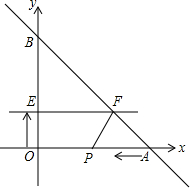 移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点.(当A运动到点O时,动直线EF随之停止运动) 连接FP,设动点P与动直线EF同时出发,运动时间为t秒.
移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点.(当A运动到点O时,动直线EF随之停止运动) 连接FP,设动点P与动直线EF同时出发,运动时间为t秒.科目:gzsx 来源: 题型:
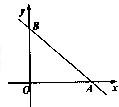 如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.
如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.| 1 | 3 |
科目:gzsx 来源: 题型:
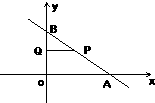 如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点.且PQ∥OA交OB于点Q.
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点.且PQ∥OA交OB于点Q.科目:czsx 来源: 题型:013
如图直线上有三个不同的点A、B、C,且AB≠BC,那么到A、B、C三点距离之和最小的点是
[ ]
科目:gzsx 来源: 题型:044
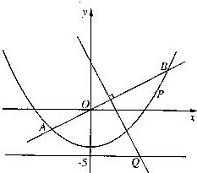
如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.
科目:gzsx 来源:数学教研室 题型:044
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.
