
科目:czsx 来源:山东省菏泽市2010年初中学业水平考试数学试题 题型:022
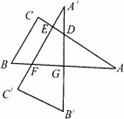
如图,三角板ABC的两直角边AC,BC的长分别为40 cm和30 cm,点G在斜边AB上,且BG=30 cm,将这个三角板以G为中心按逆时针旋转90°至△![]() 的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为________.
的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为________.
科目:czsx 来源: 题型:044
如图所示,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似,并说明理由.

科目:czsx 来源: 题型:
 如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.
如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.科目:czsx 来源:2014人教版八年级上册(专题训练 状元笔记)数学:第13章轴对称 题型:044
如图,在△ABC中,AB=AC,点D、E、F分别在边AB、BC、AC上,且BE=CF,AD+EC=AB
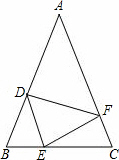
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.
科目:czsx 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:044
如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB、AC为边作等腰直角三角形ABD和等腰直角三角形ACE,使∠BAD=∠CAE=90°.

(1)求∠DBC的度数;
(2)求证:BD=CE.
科目:czsx 来源:2014浙教版八年级上册(专题训练 状元笔记)数学:第2章 特殊三角形 浙教版 题型:044
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.
科目:czsx 来源: 题型:
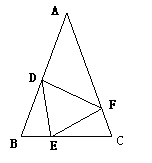
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,
BD=CE。
(1)求证:△DEF是等腰三角形;(3分)
(2)当∠A=40°时,求∠DEF的度数;(3分)
(3)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由。
(3分)
科目:czsx 来源: 题型:
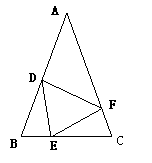
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,
BD=CE。
(1)求证:△DEF是等腰三角形;(3分)
(2)当∠A=40°时,求∠DEF的度数;(3分)
(3)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由。
(3分)
科目:czsx 来源:2015-2016学年湖南省湘潭县八年级上学期期末联考数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BE=CF,AD+EC=AB.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求 ∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
科目:czsx 来源: 题型:022
问题:探索等腰三角形—腰上的高与底边所成的角与顶角的关系.

(1)为了解决这个问题,我们可从特殊情形入手,如图①,在△ABC中,AB=AC,∠A=40°,BD是边AC上的高,则∠DBC=________°.如图②,在△ABC中,AB=AC,∠A=90°,BD是边AC上的高,则∠DBC=________°.如图③,在△ABC中,AB=AC,∠A=120°,BD是边AC上的高,则∠DBC=________°;
(2)猜想,∠A与∠DBC的关系是________;
(3)对上述猜想,你能作出解释吗?(提示:作AE⊥BC,垂足为E)
科目:czsx 来源: 题型:
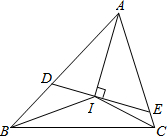 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.| ∠BAC的度数 | 40° | 60° | 90° | 120° |
| ∠BIC的度数 | ||||
| ∠BDI的度数 |
科目:czsx 来源: 题型:解答题
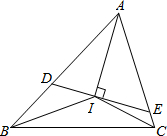 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.| ∠BAC的度数 | 40° | 60° | 90° | 120° |
| ∠BIC的度数 | ||||
| ∠BDI的度数 |
科目:czsx 来源:2015-2016学年江苏省八年级上第14周周练数学卷(解析版) 题型:解答题
背景介绍:勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
小试牛刀:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,
∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:

S梯形ABCD= ,
S△ABC= ,
S四边形AECD= ,
则它们满足的关系式为 经化简,可得到勾股定理.
知识运用:
(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
知识迁移:借助上面的思考过程与几何模型,求代数式
 的最小值(0<x<16)
的最小值(0<x<16)
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
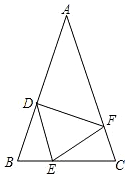 如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.科目:czsx 来源: 题型:
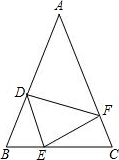 如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.科目:czsx 来源: 题型:
 时,△ADE是等腰三角形.
时,△ADE是等腰三角形. 科目:czsx 来源: 题型:
 如图,在△ABC中,AB=30,BC=40,AC=50,点D是AC上一点且3AD=2CD,过点D画线段DE,使点E在△ABC的边上且点D,E与△ABC的一个顶点组成的小三角形与△ABC相似,则满足条件的线段DE的长度分别为
如图,在△ABC中,AB=30,BC=40,AC=50,点D是AC上一点且3AD=2CD,过点D画线段DE,使点E在△ABC的边上且点D,E与△ABC的一个顶点组成的小三角形与△ABC相似,则满足条件的线段DE的长度分别为