意AB为直径的圆O 交AC 于点D E是BC 的中点答案解析
科目:czsx
来源:2016-2017学年河南省八年级上学期第三次学情调研数学试卷(解析版)
题型:单选题
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于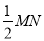 的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中错误的个数有( )
的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中错误的个数有( )

①AD平分∠BAC; ②作图依据是SAS.; ③∠ADC=60°; ④点D在AB的垂直平分线上;
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:czsx
来源:
题型:
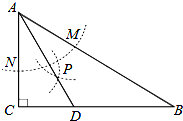
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC.
查看答案和解析>>
科目:czsx
来源:[同步]2014年北师大版初中数学七年级下第三章3.4练习卷(解析版)
题型:选择题
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC.
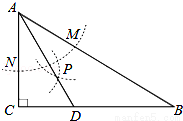
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
MN的长为半径画弧,再画弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S
△ABD=2S
△ADC.其中结论正确的序号为
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于 点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC.

A. 1 B.2 C.3 D. 4
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:czsx
来源:
题型:选择题
8.
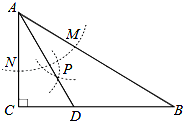
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.
查看答案和解析>>
科目:czsx
来源:
题型:选择题
16.

如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
| A. | AD是∠BAC的平分线 | | B. | ∠ADC=60° |
| C. | 点D是AB的垂直平分线上 | | D. | 如果CD=2,AB=7,则可得S△ABD=14 |
查看答案和解析>>
科目:czsx
来源:2015-2016学年山东省泰安市新泰市八年级上学期期末数学试卷(解析版)
题型:选择题
(2015秋•新泰市期末)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.
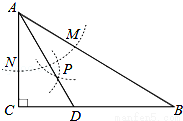
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:czsx
来源:2012年河北省唐山市开平区中考数学一模试卷(解析版)
题型:解答题
如图,△ABC中,AB>AC,AD平分∠BAC,且交BC于点D,在AB上截取AE=AC,过点E作EF∥BC交AD于点F.
(1)求证:①△ADE≌△ADC; ②四边形CDEF是菱形.
(2)求证:△ACF∽△ABD;
(3)请你以线段AE为直径作圆(只保留作图痕迹,不写作法),若所作的圆交DF于点H,小明认为点H是线段DF的中点.你同意他的观点吗?请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:选择题
1.
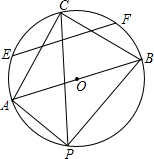
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
| A. | 4$\sqrt{3}$ | | B. | 2$\sqrt{3}$ | | C. | 6 | | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:czsx
来源:
题型:
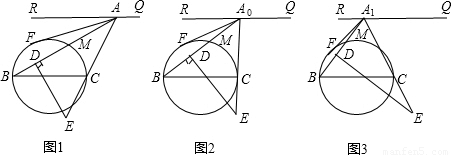
如图1,已知BC是圆O的直径,线段RQ∥BC,A是RQ上的任意一点,AF与圆O相切于点F,连接AB与圆O相交于点M,D是AB上一点,AD=AF,DE垂直于AB并与AC的延长线交于点E.
(1)当点A处于图2中A
0的位置时,A
0C与圆O相切于点C,求证:△A
0DE≌△A
0CB;
(2)当点A处于图3中A
1的位置时,A
1F:A
1E=1:2,
A1C:BC=:.求角BCA
1的大小;
(3)图1中,若BC=4,RQ与BC的距离为3,那么△ADE的面积S与点A的位置有没有关系,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图1,已知BC是圆O的直径,线段RQ∥BC,A是RQ上的任意一点,AF与圆O相切于点F,连接AB与圆O相交于点M,D是AB上一点,AD=AF,DE垂直于AB并与AC的延长线交于点E.
(1)当点A处于图2中A0的位置时,A0C与圆O相切于点C,求证:△A0DE≌△A0CB;
(2)当点A处于图3中A1的位置时,A1F:A1E=1:2,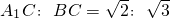 .求角BCA1的大小;
.求角BCA1的大小;
(3)图1中,若BC=4,RQ与BC的距离为3,那么△ADE的面积S与点A的位置有没有关系,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
运用“同一图形的面积用不同的表示方式”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.在解决几何问题时,我们常常用到这种“面积法”.

(1)在△ABC中,∠BAC=90°,AB=5,AC=12.请用“面积法”解决下列问题:
①如图①,若AD是BC边上的高,则AD=
;
②如图②,若⊙O是△ABC的内切圆,则⊙O的半径为
.
(2)如图2,等腰△ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB,AC的距离分别为h
1,h
2.请用面积法证明:h
1+h
2=h.
(3)如图3,在平面直角坐标系中,抛物线y=
-x
2-
x+3交x轴于A,B两点,交y轴于点C,线段BC上的一点M到AC的距离是1.请运用(2)的结论求出点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以
=
,即PC
2=PA•PB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC
2=PA•PB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:
=
.

查看答案和解析>>
科目:czsx
来源:2002年湖北省宜昌市中考数学试卷(解析版)
题型:解答题
(2002•宜昌)如图1,已知BC是圆O的直径,线段RQ∥BC,A是RQ上的任意一点,AF与圆O相切于点F,连接AB与圆O相交于点M,D是AB上一点,AD=AF,DE垂直于AB并与AC的延长线交于点E.
(1)当点A处于图2中A
的位置时,A
C与圆O相切于点C,求证:△A
DE≌△A
CB;
(2)当点A处于图3中A
1的位置时,A
1F:A
1E=1:2,

.求角BCA
1的大小;
(3)图1中,若BC=4,RQ与BC的距离为3,那么△ADE的面积S与点A的位置有没有关系,请说明理由.

查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《图形的相似》(04)(解析版)
题型:解答题
(2002•宜昌)如图1,已知BC是圆O的直径,线段RQ∥BC,A是RQ上的任意一点,AF与圆O相切于点F,连接AB与圆O相交于点M,D是AB上一点,AD=AF,DE垂直于AB并与AC的延长线交于点E.
(1)当点A处于图2中A
的位置时,A
C与圆O相切于点C,求证:△A
DE≌△A
CB;
(2)当点A处于图3中A
1的位置时,A
1F:A
1E=1:2,

.求角BCA
1的大小;
(3)图1中,若BC=4,RQ与BC的距离为3,那么△ADE的面积S与点A的位置有没有关系,请说明理由.

查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《圆》(11)(解析版)
题型:解答题
(2002•宜昌)如图1,已知BC是圆O的直径,线段RQ∥BC,A是RQ上的任意一点,AF与圆O相切于点F,连接AB与圆O相交于点M,D是AB上一点,AD=AF,DE垂直于AB并与AC的延长线交于点E.
(1)当点A处于图2中A
的位置时,A
C与圆O相切于点C,求证:△A
DE≌△A
CB;
(2)当点A处于图3中A
1的位置时,A
1F:A
1E=1:2,

.求角BCA
1的大小;
(3)图1中,若BC=4,RQ与BC的距离为3,那么△ADE的面积S与点A的位置有没有关系,请说明理由.

查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《三角形》(09)(解析版)
题型:解答题
(2002•宜昌)如图1,已知BC是圆O的直径,线段RQ∥BC,A是RQ上的任意一点,AF与圆O相切于点F,连接AB与圆O相交于点M,D是AB上一点,AD=AF,DE垂直于AB并与AC的延长线交于点E.
(1)当点A处于图2中A
的位置时,A
C与圆O相切于点C,求证:△A
DE≌△A
CB;
(2)当点A处于图3中A
1的位置时,A
1F:A
1E=1:2,
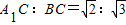
.求角BCA
1的大小;
(3)图1中,若BC=4,RQ与BC的距离为3,那么△ADE的面积S与点A的位置有没有关系,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
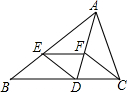
(2012•开平区一模)如图,△ABC中,AB>AC,AD平分∠BAC,且交BC于点D,在AB上截取AE=AC,过点E作EF∥BC交AD于点F.
(1)求证:①△ADE≌△ADC; ②四边形CDEF是菱形.
(2)求证:△ACF∽△ABD;
(3)请你以线段AE为直径作圆(只保留作图痕迹,不写作法),若所作的圆交DF于点H,小明认为点H是线段DF的中点.你同意他的观点吗?请说明理由.
查看答案和解析>>

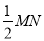 的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中错误的个数有( )
的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中错误的个数有( )
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于 点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ) 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )

 如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
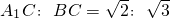 .求角BCA1的大小;
.求角BCA1的大小;


 .求角BCA1的大小;
.求角BCA1的大小;
 .求角BCA1的大小;
.求角BCA1的大小;
 .求角BCA1的大小;
.求角BCA1的大小;
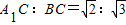 .求角BCA1的大小;
.求角BCA1的大小;
 (2012•开平区一模)如图,△ABC中,AB>AC,AD平分∠BAC,且交BC于点D,在AB上截取AE=AC,过点E作EF∥BC交AD于点F.
(2012•开平区一模)如图,△ABC中,AB>AC,AD平分∠BAC,且交BC于点D,在AB上截取AE=AC,过点E作EF∥BC交AD于点F.