如图 长方形abcd中 ab 4 bc 8.将长方形沿ef答案解析
科目:czsx
来源:同步题
题型:单选题
如图.正方形ABCD 中,AB=6,点E在边CD上,且CD= 3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④
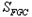
=3. 其中正确结论的个数是
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:czsx
来源:
题型:
如图,有一块边长为2
的正方形ABCD厚纸板,按照下面做法,做了一套七巧板:作图①,作对角线AC,分别取AB,BC中点E,F,连接EF作DG⊥EF于G,交AC于H,过G作GL∥BC,交AC于L,再由E作EK∥DG,交AC于K,将正方形ABCD沿画出的线剪开,现由它拼出一座桥(如图②),这座桥的阴影部分的面积是( )
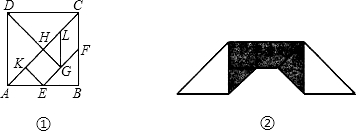
查看答案和解析>>
科目:czsx
来源:中学教材全解 七年级数学上 (北师大版) 北师大版
题型:013
如图①所示,用一块长为2的正方形ABCD厚纸板,按照下面作法,做一副七巧板:作对角线AC,分别取AB、AC中点E、F,连接EF;作DG⊥EF于G,交AC于H;过G作GL∥BC,交BC于L,再由E作EK∥DG,交AC于K,将正方形ABCD沿画出的线剪开.现用它拼出一座桥,如图②.这座桥的阴影部分面积是
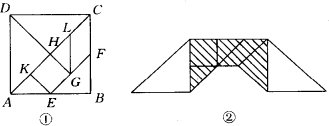
[ ]
查看答案和解析>>
科目:czsx
来源:济南
题型:单选题
如图,有一块边长为2
的正方形ABCD厚纸板,按照下面做法,做了一套七巧板:作图①,作对角线AC,分别取AB,BC中点E,F,连接EF作DG⊥EF于G,交AC于H,过G作GL
∥BC,交AC于L,再由E作EK
∥DG,交AC于K,将正方形ABCD沿画出的线剪开,现由它拼出一座桥(如图②),这座桥的阴影部分的面积是( )

查看答案和解析>>
科目:czsx
来源:
题型:
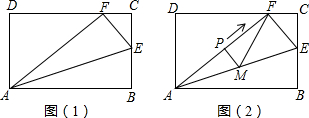
如图,矩形纸片ABCD中,AB=10cm,BC=8cm,E为BC上一点,将纸片沿AE翻折,使点E与CD边上的点F重合.
(1)求线段EF的长;
(2)若线段AF上有动点P(不与A、F重合),如图(2),点P自点A沿AF方向向点F运动,过点P作PM∥EF,PM交AE于M,连接MF,设AP=x(cm),△PMF的面积为y(cm)
2,求y与x的函数关系式;
(3)在题(2)的条件下,△FME能否是等腰三角形?若能,求出AP的值,若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,矩形纸片ABCD中,AB=10cm,BC=8cm,E为BC上一点,将纸片沿AE翻折,使点E与CD边上的点F重合.
(1)求线段EF的长;
(2)若线段AF上有动点P(不与A、F重合),如图(2),点P自点A沿AF方向向点F运动,过点P作PM∥EF,PM交AE于M,连接MF,设AP=x(cm),△PMF的面积为y(cm)2,求y与x的函数关系式;
(3)在题(2)的条件下,△FME能否是等腰三角形?若能,求出AP的值,若不能,请说明理由.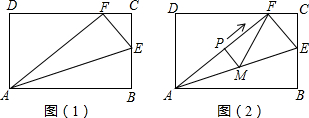
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,矩形纸片ABCD中,AB=10cm,BC=8cm,E为BC上一点,将纸片沿AE翻折,使点E与CD边上的点F重合.
(1)求线段EF的长;
(2)若线段AF上有动点P(不与A、F重合),如图(2),点P自点A沿AF方向向点F运动,过点P作PM
∥EF,PM交AE于M,连接MF,设AP=x(cm),△PMF的面积为y(cm)
2,求y与x的函数关系式;
(3)在题(2)的条件下,△FME能否是等腰三角形?若能,求出AP的值,若不能,请说明理由.
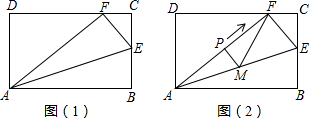
查看答案和解析>>
科目:czsx
来源:
题型:
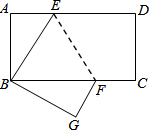
如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求BF的长.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
查看答案和解析>>
科目:czsx
来源:2009年全国中考数学试题汇编《图形的对称》(04)(解析版)
题型:解答题
(2009•遵义)如图,矩形纸片ABCD中,AB=10cm,BC=8cm,E为BC上一点,将纸片沿AE翻折,使点E与CD边上的点F重合.
(1)求线段EF的长;
(2)若线段AF上有动点P(不与A、F重合),如图(2),点P自点A沿AF方向向点F运动,过点P作PM∥EF,PM交AE于M,连接MF,设AP=x(cm),△PMF的面积为y(cm)
2,求y与x的函数关系式;
(3)在题(2)的条件下,△FME能否是等腰三角形?若能,求出AP的值,若不能,请说明理由.

查看答案和解析>>
科目:czsx
来源:2009年贵州省遵义市中考数学试卷(解析版)
题型:解答题
(2009•遵义)如图,矩形纸片ABCD中,AB=10cm,BC=8cm,E为BC上一点,将纸片沿AE翻折,使点E与CD边上的点F重合.
(1)求线段EF的长;
(2)若线段AF上有动点P(不与A、F重合),如图(2),点P自点A沿AF方向向点F运动,过点P作PM∥EF,PM交AE于M,连接MF,设AP=x(cm),△PMF的面积为y(cm)
2,求y与x的函数关系式;
(3)在题(2)的条件下,△FME能否是等腰三角形?若能,求出AP的值,若不能,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.已知正方形ABCD,探究以下问题:
(1)如图1,点F在BC上,作FE⊥BD于点E,取DF的中点G,连接EG、CG,将△EGC沿直线EC翻折到△EG′C,求证:四边形EGCG′是菱形;
(2)如图2,点F是BC外一点,作FE⊥BC于点E,且BE=EF,连接DF,取DF的中点G,将△EGC沿直线EC翻折到△EG′C,作FM⊥CD于点M,请问(1)中的结论”四边形EGCG′是菱形”是否依然成立,并说明理由;
(3)在(2)的条件下,若图2中AB=4,设BE长为x,四边形EGCG′的面积为S,请求出S关于x的函数关系式,并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,
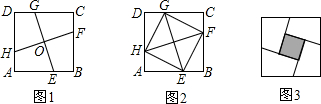
HA=EB=FC=GD=1cm,则图3中阴影部分的面积为
cm
2.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,B是长度为1的线段AE上任意一点,在AE的同一侧分别作正方形ABCD和长方形BEFG,且EF=2BE.
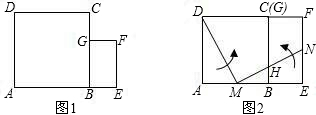
(1)点B在何处时,正方形ABCD的面积与长方形BEFG的面积和最小,最小值为多少?
(2)若点C与点G重合,M为AB中点,N为EF中点,MN与BC交于点H(如图2所示),将△OMA沿直线DM,△MNE沿直线MN分别向矩形AEFD内折叠,求四边形DMNF未被两个折叠三角形覆盖的图形面积.
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,用一块边长为2
的正方形ABCD厚纸板,按下面的做法做一套七巧板:作对角线AC,分别取AB、BC的中点E、F,连接EF;连接BD,交EF于G,交AC于H;将正方形ABCD沿画出的线剪开,现把它们拼成一座桥,如图(2)所示,这座桥阴影部分的面积是( )
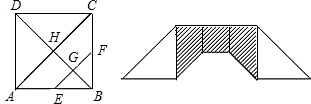
查看答案和解析>>
科目:czsx
来源:
题型:
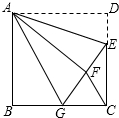
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S
△FGC=3.其中正确结论的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,正方形ABCD中,有一直径为BC=2cm 的半圆O.两点E、F分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动.设点E离开点的B时间为t(s),其中1≤t<2.
(1)当t为何值时,线段EF和BC平行?
(2)EF能否与半圆O相切?如果能,求出t的值;如果不能,请说明原因.
(3)如图2,设EF与AC相交于点P,当点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,也请说明理由,并求AP:PC的值.
变式:如图3,若将上题改为,正方形ABCD中,有一直径为BC=2cm的半圆O.点E为AB边上的动点(不与点A、B重合),过点E与圆O相切的直线交CD所在直线为点F,设EB=x,FD=y.
(1)试写出y关于x的函数关系式,并写出自变量x的取值范围.
(2)是否存在切线EF,把正方形ABCD的周长分成相等的两部分?若存在,求出x的值.若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
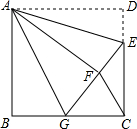
如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则GC=
6
6
.
查看答案和解析>>
科目:czsx
来源:
题型:
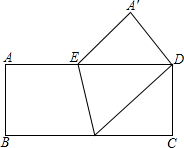
如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置.
(1)求DE的长度;
(2)试说明DE=DF的理由;
(3)求EF的长度.
查看答案和解析>>
科目:czsx
来源:
题型:
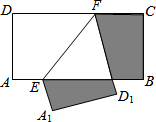
如图,在长方形纸片ABCD中,AB=2,BC=1,点E、F分别在AB、CD上,将纸片沿EF折叠,使点A、D分别落在点A
1、D
1处,则阴影部分图形的周长为( )
查看答案和解析>>

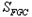 =3. 其中正确结论的个数是
=3. 其中正确结论的个数是 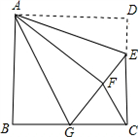
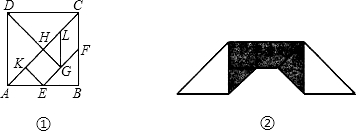





 如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处. 如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.


 HA=EB=FC=GD=1cm,则图3中阴影部分的面积为
HA=EB=FC=GD=1cm,则图3中阴影部分的面积为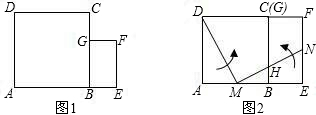

 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
 如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则GC=
如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则GC= 如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置.
如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置. 如图,在长方形纸片ABCD中,AB=2,BC=1,点E、F分别在AB、CD上,将纸片沿EF折叠,使点A、D分别落在点A1、D1处,则阴影部分图形的周长为( )
如图,在长方形纸片ABCD中,AB=2,BC=1,点E、F分别在AB、CD上,将纸片沿EF折叠,使点A、D分别落在点A1、D1处,则阴影部分图形的周长为( )