
科目:gzsx 来源:2010年吉林省高一上学期期末考试数学卷 题型:选择题
设 a、b 是两个不同的平面,给出下列命题:
① 若平面 a 内的直线 l垂直于平面 b 内的任意直线,则 a⊥b
② 若平面 a 内的任一直线都平行于平面 b,则 a//b
③ 若平面 a 垂直于平面 b,直线 l 在平面 a 内,则 l⊥b
④ 若平面 a 平行于平面 b,直线 l 在平面 a 内,则 l//b
其中正确命题的个数是 ( )
A.4 B.3 C.2 D.1
科目:gzsx 来源:不详 题型:单选题
| A.4 | B.3 | C.2 | D.1 |
科目:gzsx 来源: 题型:单选题
设 a、b是两个不同的平面,给出下列命题:
① 若平面 a内的直线 l垂直于平面 b内的任意直线,则 a⊥b
② 若平面 a内的任一直线都平行于平面 b,则 a//b
③ 若平面 a垂直于平面 b,直线 l 在平面 a内,则 l⊥b
④ 若平面 a平行于平面 b,直线 l 在平面 a内,则 l//b
其中正确命题的个数是
科目:gzsx 来源: 题型:
设 a、b 是两个不同的平面,给出下列命题:
① 若平面 a 内的直线 l垂直于平面 b 内的任意直线,则 a⊥b
② 若平面 a 内的任一直线都平行于平面 b,则 a//b
③ 若平面 a 垂直于平面 b,直线 l在平面 a 内,则 l⊥b
④ 若平面 a 平行于平面 b,直线 l 在平面 a 内,则 l//b
其中正确命题的个数是 ( )
A.4 B.3 C.2 D.1
科目:gzsx 来源: 题型:选择题
| A. | α⊥β | B. | α与β不垂直 | C. | l0⊥a | D. | l0⊥m |
科目:gzsx 来源: 题型:选择题
| A. | 若l⊂α,m不平行于l,则m不平行于α | |
| B. | 若l⊂α,m⊂β,且α,β不平行,则l,m不平行 | |
| C. | 若l⊂α,m不垂直于l,则m不垂直于α | |
| D. | 若l⊂α,m⊂β,l不垂直于m,则α,β不垂直 |
科目:gzsx 来源: 题型:
在平面直角坐标系xOy中,经过点(0,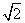 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q.
(1)求k的取值范围;
(2)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量 +
+ 与
与 垂直?如果存在,求k值;如果不存在,请说明理由.
垂直?如果存在,求k值;如果不存在,请说明理由.
科目:gzwl 来源: 题型:

科目:czsx 来源:江苏省无锡市天一实验学校2012届九年级一模数学试题 题型:044
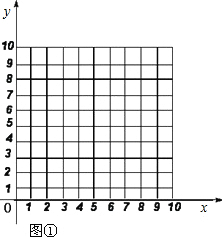
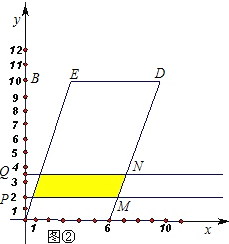
在平面直角坐标系中,点B的坐标为(0,10),点P、Q同时从O点出发,在线段OB上做往返运动,点P往返一次需10 s,点Q往返一次需6 s.设动点P、Q运动的时间为x( s),动点离开原点的距离是y.
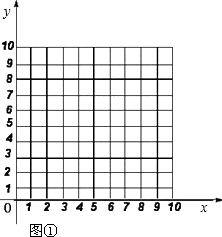
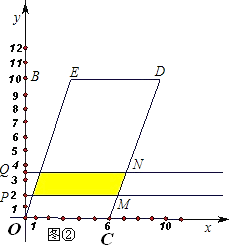
(1)当0≤x≤10时,在图①中,分别画出点P、点Q运动时关于x的函数图象,并回答:
①点P从O点出发,1个往返之间与点Q相遇几次(不包括O点)?
②点P从O点出发,几秒后与点Q第一次相遇?
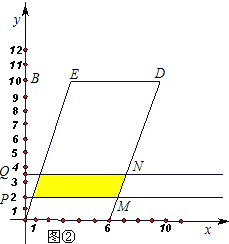
(2)如图②,在平面直角坐标系中,□OCDE的顶点C(6,0),D、E、B在同一直线上.分别过点P、Q作PM、QN垂直于y轴,P、Q为垂足.设运动过程中两条直线PM,QN与□OCDE围成图形(阴影部分)的面积是S,试求当x(0≤x≤5)为多少秒时,S有最大值.最大值是多少?
科目:gzsx 来源: 题型:
科目:gzwl 来源:2015-2016学年重庆巴蜀中学高一上期期末物理卷(解析版) 题型:选择题
如图所示,倾角为30o的斜面固定在水平地面上。两根相同的光滑细钉(大小不计)垂直斜面对称固定在斜面底边中垂线OO'的两侧,相距l,将一遵循胡克定律、劲度系数为k的轻质弹性绳套套在两个细钉上时,弹性绳恰好处于自然伸长状态。现将一物块通过光滑轻质挂钩挂在绳上并置于斜面上的A位置,物块在沿斜面向下的外力作用下才能缓慢沿OO'向下移动。当物块运动至B位置时撤去外力,物块处于静止状态。已知AB=l,轻绳始终与斜面平行,设最大静摩擦力等于滑动摩擦力,下列说法正确的是

A.物块到达B位置时,弹性绳的形变量为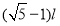
B.在移动物块的过程中,斜面对物体的作用力保持不变,且为
C.撤去外力后,物块在B位置受到的摩擦力可能小于
D.物体从A位置到达B位置的过程中,物体受到的摩擦力都沿斜面向上
科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(3,4),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).
如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(3,4),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).科目:czsx 来源: 题型:
科目:czsx 来源:重庆市开县中学2010届初三下学期“两考合一”模拟考试数学试题 题型:059
如图,在平面直角坐标系中,四边形OABC是梯形,OA∥CB,点A坐标为(6,0),点B坐标为(3,4),点C在y轴的正半轴上,动点M在OA边上运动,从O点出发到A点;动点N在AB边上运动,从A点出发到B点,两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也就随即停止,设两点的运动时间为t(秒).
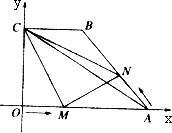
(1)求线段AB的长;并求当t为何值时,MN∥OC?
(2)设△CMN的面积为S,求S与t之间的函数解析式,并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?
(3)连接CA,那么是否存在这样的t值,使MN与AC互相垂直?若存在,求出这时的t值,若不存在,请说明理由.
科目:czsx 来源:2009年云南省昆明中考数学试题及答案 题型:059
如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(4,3),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).

(1)求线段AB的长;当t为何值时,MN∥OC?
(2)设△CMN的面积为S,求S与t之间的函数解析式,并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?
(3)连接AC,那么是否存在这样的t,使MN与AC互相垂直?若存在,求出这时的t值;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
 个单位长度,过P作x轴的平行线交AB于点N,设点P的运动时间为t,线段AN长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
个单位长度,过P作x轴的平行线交AB于点N,设点P的运动时间为t,线段AN长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;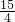 个单位长度,设P、Q两点同时出发,当一点到达终点时另一点停止运动,连接ON,当AD平分线段NQ时,求此时t的值.
个单位长度,设P、Q两点同时出发,当一点到达终点时另一点停止运动,连接ON,当AD平分线段NQ时,求此时t的值.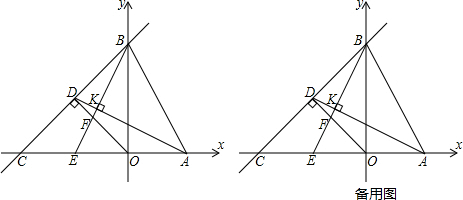
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
 x+3分别与x轴、y轴分别交于点A、点B.动点P、Q分别从O、A同时出发,其中点P以每秒1个点位长度的速度沿OA方向向A点匀速运动,到达A点后立即以原速度沿AO返向;点Q以每秒1个单位长度的速度从A点出发,沿A-B-O方向向O点匀速运动.当点Q到达点O时,P、Q两点同时停止运动.设运动时间为t(秒).
x+3分别与x轴、y轴分别交于点A、点B.动点P、Q分别从O、A同时出发,其中点P以每秒1个点位长度的速度沿OA方向向A点匀速运动,到达A点后立即以原速度沿AO返向;点Q以每秒1个单位长度的速度从A点出发,沿A-B-O方向向O点匀速运动.当点Q到达点O时,P、Q两点同时停止运动.设运动时间为t(秒).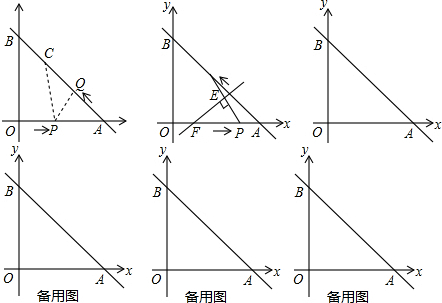
科目:czsx 来源: 题型:解答题
 请说明理由.
请说明理由.科目:czsx 来源: 题型:
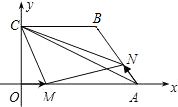
如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(4,3),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).
(1)求线段AB的长;当t为何值时,MN∥OC?
(2)设△CMN的面积为S,求S与t之间的函数解析式,并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?
(3)连接AC,那么是否存在这样的t,使MN与AC互相垂直?若存在,求出这时的t值;若不存在,请说明理由.
