精英家教网 >
试题搜索列表 >如图1.点E.F分别在正方形ABCD的边BC.CD上.∠EAF=45°.连接EF.则EF=BE+DF.试说明理由,
如图1.点E.F分别在正方形ABCD的边BC.CD上.∠EAF=45°.连接EF.则EF=BE+DF.试说明理由,答案解析
科目:czsx
来源:
题型:
(1)问题发现
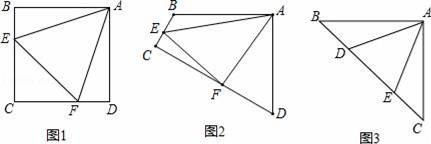
如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.

查看答案和解析>>
科目:czsx
来源:2016届四川省自贡市六校中考二模数学试卷(解析版)
题型:解答题
倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答
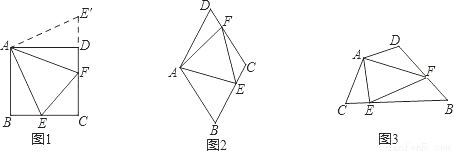
习题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
【解析】
∵正方形ABCD中,AB=AD,∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°-45°=45°=∠EAF.
又∵AE′=AE,AF=AF
∴△AE′FF≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究.
观察分析:
观察图1,由解答可知,该题有用的条件是①.ABCD是四边形,点E、F分别在边BC、CD上;②.AB=AD;③.∠B=∠D=90°∠;④.∠EAF= ∠BAD.
∠BAD.
类比猜想:
在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
要解决上述问题,可从特例入手,请同学们思考:如图2,在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?试证明.
(2)在四边形ABCD中,点E、F分别在边BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF= ∠BAD时,还有EF=BE+DF吗?使用图3证明.
∠BAD时,还有EF=BE+DF吗?使用图3证明.
归纳概括:
反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题: .
查看答案和解析>>
科目:czsx
来源:
题型:解答题
2.(1)问题背景
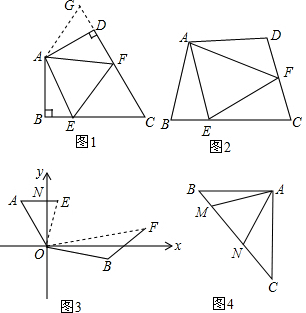
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是EF=BE+DF;
(2)探索延伸
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=$\frac{1}{2}$∠BAD,上述结论是否仍然成立,并说明理由;
(3)结论应用
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
(4)能力提高
如图4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
20.倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答
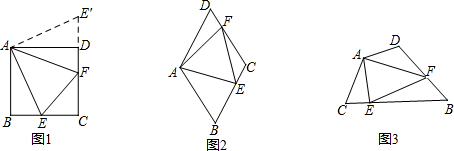
习题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解:
∵正方形ABCD中,AB=AD,∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°-45°=45°=∠EAF.
又∵AE′=AE,AF=AF
∴△AE′FF≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究.
观察分析:
观察图1,由解答可知,该题有用的条件是①.ABCD是四边形,点E、F分别在边BC、CD上;②.AB=AD;③.∠B=∠D=90°∠;④.∠EAF=$\frac{1}{2}$∠BAD.
类比猜想:
在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
要解决上述问题,可从特例入手,请同学们思考:如图2,在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?试证明.
(2)在四边形ABCD中,点E、F分别在边BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=$\frac{1}{2}$∠BAD时,还有EF=BE+DF吗?使用图3证明.
归纳概括:
反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题:在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=$\frac{1}{2}$∠BAD时,EF=BE+DF.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(四川达州卷)数学(解析版)
题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。
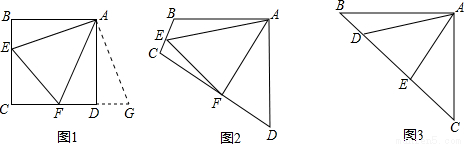
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据 ,易证△AFG≌ ,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。
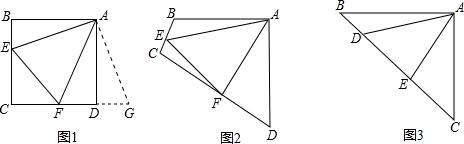
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据
,易证△AFG≌
,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系
时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
查看答案和解析>>
科目:czsx
来源:2013-2014学年辽宁省盘锦市中考第一次模拟考试数学试卷(解析版)
题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,∴∠FDG=180°,点F、D、G共线。
根据__ __________,易证△AFG≌_ _______,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系_ ___时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。

查看答案和解析>>
科目:czsx
来源:2013年四川省达州市中考数学试卷(解析版)
题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
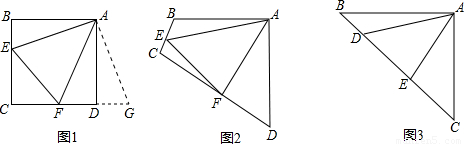
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据______,易证△AFG≌______,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:
题型:
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整并解答.
原题:(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(2)类比引申
如图2,四边形
ABCD中,
AB=
AD,∠
BAD=90°,点
E、
F分别在边
BC、
CD 上,∠
EAF=45°.若∠
B、∠
D都不是直角,则当∠
B与∠
D满足等量关系
时,仍有
EF=
BE+
DF.说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
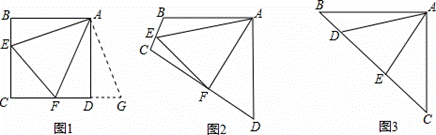
(1)思路梳理
∵AB=CD, ∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°, ∴∠FDG=180°,点F、D、G共线.
根据 ,易证△AFG≌ ,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:2015-2016学年江苏省江阴市八年级下第一次月考数学试卷(解析版)
题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___________,SAS
易证△AFG≌___________△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°.点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______________∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:2015-2016学年湖北宜昌八年级下八校(3月)联考数学卷(解析版)
题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,
连接EF,则EF=BE+DF,试说明理由.

(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°
∴点F、D、G共线
根据 ,易证△AFG≌ ,进而得EF=BE+DF.
(2)联想拓展
如图2,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的数量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
4.通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.

(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据SAS,易证△AFG≌GAF,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.
若∠B、∠D都不是直角,则当∠B与∠D满足等量关系∠B+∠ADC=180° 时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
3.通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.
下面是一个案例,请补充完整.
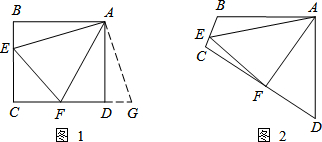
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°,点F、D、G共线根据SAS,易证△AFG≌△AFE,从而可得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系∠B+∠D=180°时,仍有EF=BE+DF.
请写出推理过程:
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•达州)通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
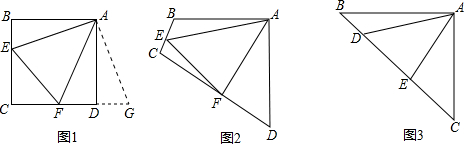
(1)思路梳理
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据
SAS
SAS
,易证△AFG≌
△AEF
△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系
∠B+∠D=180°
∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
15.我们可以通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
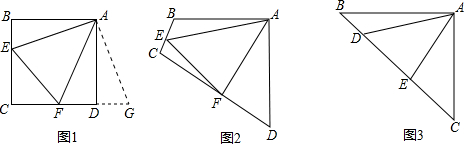
(1)思路梳理
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据SAS,易证△AFG≌△AFG,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系∠B+∠D=180°时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:czsx
来源:2015-2016学年湖南省衡阳市八年级上学期期中数学试卷(解析版)
题型:解答题
(2015秋•衡阳校级期中)通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.
下面是一个案例,请补充完整.
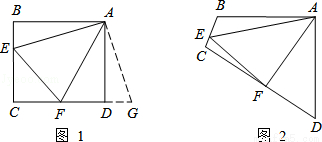
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°,点F、D、G共线根据SAS,易证△AFG≌ ,从而可得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF.
请写出推理过程:
查看答案和解析>>



 ∠BAD.
∠BAD. ∠BAD时,还有EF=BE+DF吗?使用图3证明.
∠BAD时,还有EF=BE+DF吗?使用图3证明.














