抛物线y2=x上存在P,Q两点关于直线y-1=k答案解析
科目:gzsx
来源:
题型:

已知抛物线C:y
2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)在抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由;
(3)设G,H是抛物线C上异于原点O的两个不同点,且
•
=0,求△GOH面积的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
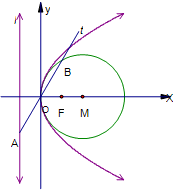 如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)设G,H是抛物线C上异于原点O的两个不同点,且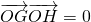 ,求△GOH面积的最小值;
,求△GOH面积的最小值;
(3)在抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
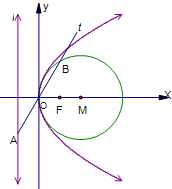 如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)试探究抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:《圆锥曲线》2013年广东省十二大市高三二模数学试卷汇编(理科)(解析版)
题型:解答题
如图已知抛物线C:y
2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为

的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)设G,H是抛物线C上异于原点O的两个不同点,且

,求△GOH面积的最小值;
(3)在抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.

查看答案和解析>>
科目:gzsx
来源:2013年广东省揭阳市高考数学二模试卷(文科)(解析版)
题型:解答题
如图已知抛物线C:y
2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为

的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)试探究抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.

查看答案和解析>>
科目:gzsx
来源:2013年广东省揭阳市高考数学二模试卷(理科)(解析版)
题型:解答题
如图已知抛物线C:y
2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为

的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)设G,H是抛物线C上异于原点O的两个不同点,且

,求△GOH面积的最小值;
(3)在抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
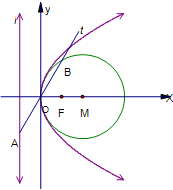
(2013•揭阳二模)如图已知抛物线C:y
2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)设G,H是抛物线C上异于原点O的两个不同点,且
•=0,求△GOH面积的最小值;
(3)在抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
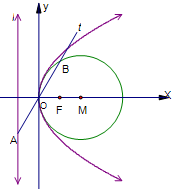
(2013•揭阳二模)如图已知抛物线C:y
2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
(1)求圆M和抛物线C的方程;
(2)试探究抛物线C上是否存在两点P,Q关于直线m:y=k(x-1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在平面直角坐标系中,O为坐标原点,已知抛物线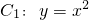 ,点A(2,4).
,点A(2,4).
(Ⅰ)求直线OA的解析式;
(Ⅱ)直线x=2与x轴相交于点B,将抛物线C1从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动,设抛物线顶点M的横坐标为m.
①当m为何值时,线段PB最短?
②当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由;
(Ⅲ)将抛物线C1作适当的平移,得抛物线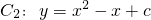 ,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
查看答案和解析>>
科目:czsx
来源:2012年天津市和平区中考数学一模试卷(解析版)
题型:解答题
在平面直角坐标系中,O为坐标原点,已知抛物线

,点A(2,4).
(Ⅰ)求直线OA的解析式;
(Ⅱ)直线x=2与x轴相交于点B,将抛物线C
1从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动,设抛物线顶点M的横坐标为m.
①当m为何值时,线段PB最短?
②当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由;
(Ⅲ)将抛物线C
1作适当的平移,得抛物线

,若点D(x
1,y
1),E(x
2,y
2)在抛物线C
2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x2+4x-3交x轴于A,B两点(点A在点B的左边),交y轴于C点.
(1)求直线BC的解析式;
(2)已知点M在线段BC上运动(不与点B,C重合),将OM绕点O逆时针转90°到OM′的位置,当点M′落在抛物线上时,求点M的坐标;
(3)将抛物线向左平移3个单位,得到抛物线y0,已知点P(2a,y1)、M(4a,y2)、N(7a,y3)都在抛物线y0上,是否存在含有y1,y2,y3,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
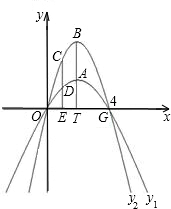
经过原点和G(4,0)的两条抛物线y
1=a
1x
2+b
1x,y
2=a
2x
2+b
2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
(1)分别求出抛物线y
1和y
2的解析式;
(2)点C是抛物线y
2的x轴上方的一动点,作CE⊥x轴于E,交抛物线y
1于D,试判断CD和DE的数量关系,并说明理由;
(3)直线x=m,交抛物线y
1于M,交抛物线y
2于N,是否存在以点M,N,B,T为顶点的四边形是平行四边形,若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
(1)分别求出抛物线y1和y2的解析式;
(2)点C是抛物线y2的x轴上方的一动点,作CE⊥x轴于E,交抛物线y1于D,试判断CD和DE的数量关系,并说明理由;
(3)直线x=m,交抛物线y1于M,交抛物线y2于N,是否存在以点M,N,B,T为顶点的四边形是平行四边形,若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:2011年江西省中考数学试卷(样卷四)(解析版)
题型:解答题
经过原点和G(4,0)的两条抛物线y
1=a
1x
2+b
1x,y
2=a
2x
2+b
2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
(1)分别求出抛物线y
1和y
2的解析式;
(2)点C是抛物线y
2的x轴上方的一动点,作CE⊥x轴于E,交抛物线y
1于D,试判断CD和DE的数量关系,并说明理由;
(3)直线x=m,交抛物线y
1于M,交抛物线y
2于N,是否存在以点M,N,B,T为顶点的四边形是平行四边形,若存在,求出m的值;若不存在,说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
(2012•和平区一模)在平面直角坐标系中,O为坐标原点,已知抛物线C1:y=x2,点A(2,4).
(Ⅰ)求直线OA的解析式;
(Ⅱ)直线x=2与x轴相交于点B,将抛物线C1从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动,设抛物线顶点M的横坐标为m.
①当m为何值时,线段PB最短?
②当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由;
(Ⅲ)将抛物线C1作适当的平移,得抛物线C2:y=x2-x+c,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
查看答案和解析>>
科目:czsx
来源:2016届江西省景德镇市中考二模数学试卷(解析版)
题型:解答题
如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1= (x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(1)求A,B,C三点的坐标和曲线y2的表达式;
(2)我们把其中一条对角线被另一条对角线垂直且平分的四边形称为筝形.过点C作x轴的平行线与曲线y1交于另一个点D,连接AD.试问:在曲线y2上是否存在一点M,使得四边形ACDM为筝形?若存在,计算出点M的横坐标,若不存在,说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.

如图形似“w”的函数是由抛物线y
1的一部分,其表达式为:y
1=$\frac{\sqrt{3}}{3}$(x
2-2x-3)(x≤3)以及抛物线y
2的一部分所构成的,其中曲线y
2与曲线y
1关于直线x=3对称,A、B是曲线y
1与x轴两交点(A在B的左边),C是曲线y
1与y轴交点.
(1)求A,B,C三点的坐标和曲线y
2的表达式;
(2)我们把其中一条对角线被另一条对角线垂直且平分的四边形称为筝形.过点C作x轴的平行线与曲线y
1交于另一个点D,连接AD.试问:在曲线y
2上是否存在一点M,使得四边形ACDM为筝形?若存在,计算出点M的横坐标,若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知直线
y1=-x+与x、y轴分别交于A、B两点,抛物线
y2=-x2+bx+c
过A、B两点,
①求抛物线的解析式;
②在抛物线上是否存在一点P(除点A外),使点P关于直线
y1=-x+的对称点Q恰好在x轴上?若不存在,请说明理由;若存在,求出点P的坐标,并求得此时四边形APBQ的面积.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
6.
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W
1和W
2,若在图形W
1和W
2上分别存在点M (x
1,y
1 )和N (x
2,y
2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W
1和W
2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
(1)已知点A(0,1),B(4,1),C(3,-1),D(3,-2),连接AB,CD.
①对于线段AB和线段CD,若点A和C被点P“关联”,则点P的坐标为($\frac{3}{2}$,0);
②线段AB和线段CD的一“中位点”是Q (2,-$\frac{1}{2}$),求这两条线段上被点Q“关联”的两个点的坐标;
(2)如图1,已知点R(-2,0)和抛物线W
1:y=x
2-2x,对于抛物线W
1上的每一个点M,在抛物线W
2上都存在点N,使得点N和M 被点R“关联”,请在图1 中画出符合条件的抛物线W
2;
(3)正方形EFGH的顶点分别是E(-4,1),F(-4,-1),G(-2,-1),H(-2,1),⊙T的圆心为T(3,0),半径为1.请在图2中画出由正方形EFGH和⊙T的所有“中位点”组成的图形(若涉及平面中某个区域时可以用阴影表示),并直接写出该图形的面积.
查看答案和解析>>
科目:czsx
来源:2013-2014学年山东泰州市姜堰区九年级第一学期期末调研数学试卷(解析版)
题型:解答题
已知,关于x的二次函数, (k为正整数).
(k为正整数).

(1)若二次函数 的图象与x轴有两个交点,求k的值.
的图象与x轴有两个交点,求k的值.
(2)若关于x的一元二次方程 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 (k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(3)将(2)中的抛物线平移,当顶点至原点时,直线y=2x+b交抛物线于A(-1,n)、B(2,t)两点,问在y轴上是否存在一点C,使得△ABC的内心在y轴上.若存在,求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>

 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. ,求△GOH面积的最小值;
,求△GOH面积的最小值; 如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. ,求△GOH面积的最小值;
,求△GOH面积的最小值;
 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. ,求△GOH面积的最小值;
,求△GOH面积的最小值;
 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为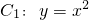 ,点A(2,4).
,点A(2,4). ,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围. ,点A(2,4).
,点A(2,4). ,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围. 经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3. 经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
 (x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
 如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=$\frac{\sqrt{3}}{3}$(x2-2x-3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=$\frac{\sqrt{3}}{3}$(x2-2x-3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点. 过A、B两点,
过A、B两点, 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$ (k为正整数).
(k为正整数).
 的图象与x轴有两个交点,求k的值.
的图象与x轴有两个交点,求k的值. (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 (k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.