
科目:czsx 来源: 题型:
在数学活动课上,老师提出了一个问题,希望同学们进行探究.
在平面直角坐标系中,若一次函数 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象交于C、D两点,则AD和BC有怎样的数量关系?
的图象交于C、D两点,则AD和BC有怎样的数量关系?
同学们通过合作讨论,逐渐完成了对问题的探究.
小勇说:我们可以从特殊入手,取 进行研究(如图①),此时我发现AD=BC.
进行研究(如图①),此时我发现AD=BC.
小攀说:在图①中,分别从点C、D两点向两条坐标轴作垂线,根据所学知识可以知道有两个图形的面积是相等的,并能求出确定的值,而且在图②中,此时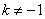 ,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
小高说:我还发现,在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是 .


图① 图②

(1)请完成以上填空;
(2)请结合以上三位同学的讨论,对图②所示的情况下,证明AD=BC;
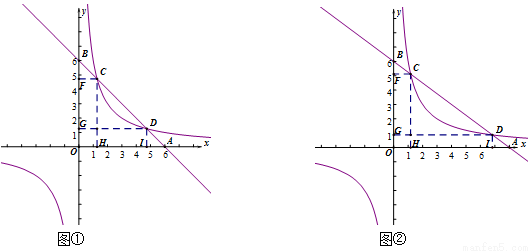
小峰突然提出一个问题:通过刚才的证明,我们可以知道当直线与双曲线的两个交点都在第一象限时, 总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
(3)请你结合小峰提出的问题,在图③中画出示意图,并判断结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
科目:czsx 来源:2016届北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:解答题
在数学活动课上,老师提出了一个问题,希望同学们进行探究.
在平面直角坐标系中,若一次函数 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象交于C、D两点,则AD和BC有怎样的数量关系?
的图象交于C、D两点,则AD和BC有怎样的数量关系?
同学们通过合作讨论,逐渐完成了对问题的探究.
小勇说:我们可以从特殊入手,取 进行研究(如图①),此时我发现AD=BC.
进行研究(如图①),此时我发现AD=BC.
小攀说:在图①中,分别从点C、D两点向两条坐标轴作垂线,根据所学知识可以知道有两个图形的面积是相等的,并能求出确定的值,而且在图②中,此时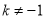 ,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
小高说:我还发现,在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是 .
(1)请完成以上填空;
(2)请结合以上三位同学的讨论,对图②所示的情况下,证明AD=BC;
小峰突然提出一个问题:通过刚才的证明,我们可以知道当直线与双曲线的两个交点都在第一象限时, 总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
(3)请你结合小峰提出的问题,在图③中画出示意图,并判断结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
科目:czsx 来源:数学教研室 题型:044
(1)写出E、F两点的坐标(用含有a ,b的代数式表示);
(2)求△OEF的面积;
(3)若P点在y=![]() 的图象上移动,则∠EOF的大小是否变化,并说明理由.
的图象上移动,则∠EOF的大小是否变化,并说明理由.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
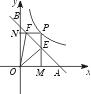
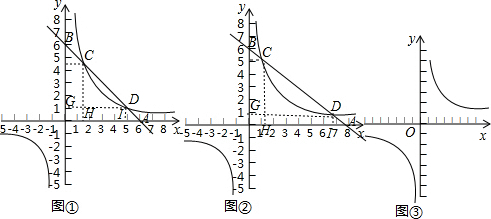
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中,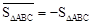 .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组(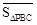 ,
,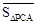 ,
,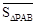 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作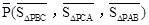 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,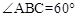 ,则
,则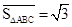 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”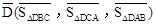 为
为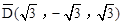 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: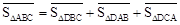 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则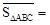 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系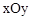 中,点
中,点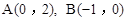 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于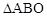 的“面积坐标”为
的“面积坐标”为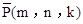 ,
,
试探究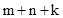 与
与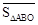 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点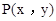 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于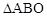 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点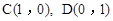 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.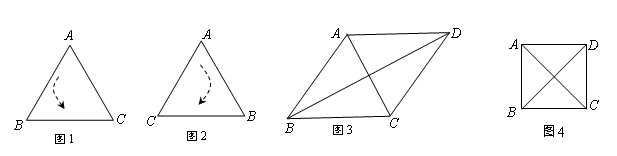
科目:czsx 来源:不详 题型:解答题
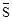 表示,例如图1中,
表示,例如图1中,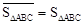 ,图2中,
,图2中,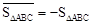 .
.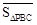 ,
,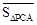 ,
,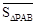 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作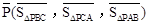 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,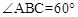 ,则
,则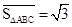 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”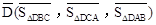 为
为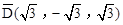 .在图3中,我们知道
.在图3中,我们知道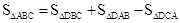 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: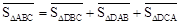 .
.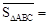 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: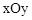 中,点
中,点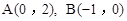 ,
,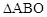 的“面积坐标”为
的“面积坐标”为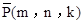 ,
,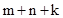 与
与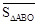 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;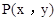 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于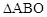 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);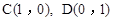 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.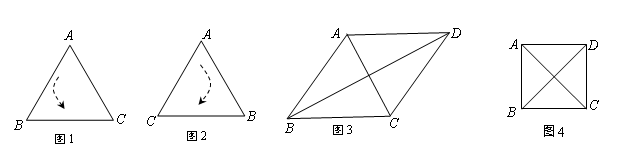
科目:czsx 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用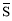 表示,例如图1中,
表示,例如图1中,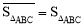 ,图2中,
,图2中, .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组( ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: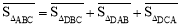 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.

科目:czsx 来源: 题型:
. |
| S |
. |
| S △ABC |
. |
| S △ABC |
. |
| S △PBC |
. |
| S △PCA |
. |
| S △PAB |
. |
| P |
. |
| S △PBC |
. |
| S △PCA |
. |
| S △PAB |
. |
| S △ABC |
| 3 |
. |
| D |
. |
| S △DBC |
. |
| S △DCA |
. |
| S △DAB |
. |
| D |
| 3 |
| 3 |
| 3 |
. |
| S △ABC |
. |
| S △DBC |
. |
| S △DAB |
. |
| S △DCA |
. |
| S △ABC |
. |
| P |
. |
| S △ABO |

科目:czsx 来源: 题型:
定义1:在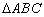 中,若顶点
中,若顶点 ,
, ,
, 按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
 ,
, ,
, 按顺时针方向排列,则规定它的面积的相反数为
按顺时针方向排列,则规定它的面积的相反数为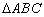 的“有向面积”。“有
的“有向面积”。“有 向面积”用
向面积”用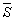 表示,
表示,


 例如图1中,
例如图1中, ,图2中,
,图2中,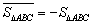 。
。
定义2:在平面内任取一个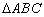 和点
和点 (点
(点 不在
不在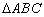 的三边所在直线上),称有序数组(
的三边所在直线上),称有序数组( ,
, ,
,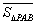 )为点
)为点 关于
关于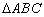 的“
的“ 面积坐标”,记作
面积坐标”,记作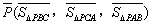 ,例如图3中,菱形
,例如图3中,菱形 的边长为2,
的边长为2, ,则
,则 ,点
,点 关于
关于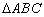 的“面积坐标”
的“面积坐标” 为
为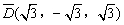 。
。
 在图3中,我们知道
在图3中,我们知道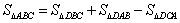 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为:
 。
。
应用新知:
(1)如图4,正方形 的边长为1,则
的边长为1,则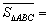 ,点
,点 关于
关于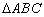 的“面积坐标”是 ;
的“面积坐标”是 ;
探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
, .
.
①若点 是第二象限内任意一点(不在直线
是第二象限内任意一点(不在直线 上),设点
上),设点 关于
关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与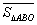 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点
是第四象限内任意一点,请直接写出点 关于
关于 的“面积坐标”(用
的“面积坐标”(用 表示);
表示);
解决问题:
(3)在(2)的条件下,点 ,
, ,点
,点 在抛物线
在抛物线 上,求当
上,求当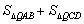 的值最小时,点
的值最小时,点 的横坐标。
的横坐标。
科目:czsx 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
已知抛物线的顶点为D(0,![]() ),且经过点A(1,
),且经过点A(1,![]() ),如下图所示.
),如下图所示.

(1)求这条抛物线的解析式;
(2)点F是坐标原点O关于该抛物线顶点D的对称点,坐标为F(0,![]() ),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴于A1,过点F作x轴的平行线,交AA1于点A2,则FA2=1,A2A=
),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴于A1,过点F作x轴的平行线,交AA1于点A2,则FA2=1,A2A=![]() -
-![]() =
=![]() ,在Rt△AFA2中,FA=
,在Rt△AFA2中,FA=![]() =
=![]() .已知抛物线上另一点B的横坐标为2,求线段FB的长;
.已知抛物线上另一点B的横坐标为2,求线段FB的长;
(3)若点P是该抛物线在第一象限内的任意一点,试探究线段FP的长度与点P纵坐标的大小关系,并证明你的猜想.
科目:czsx 来源: 题型:阅读理解
| x |
| x+2 |
| 3 | x |
| 3 | x-1 |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x+2 |
| 3 |
| x-1 |
| 3 |
| x-1 |
科目:czsx 来源: 题型:解答题
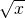 →y=3
→y=3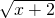 +1;y=3
+1;y=3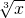 →y=3
→y=3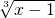 +1;y=
+1;y=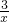 →y=
→y=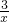 +1;…
+1;…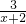 +1图象再往______平移______个单位,所得函数图象的解析式为y=
+1图象再往______平移______个单位,所得函数图象的解析式为y=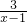 +1;
+1;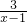 +1图象性质的描述:
+1图象性质的描述:科目:czsx 来源:2013年浙江省台州地区中考数学二模试卷(解析版) 题型:填空题
 →y=3
→y=3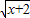 +1;y=3
+1;y=3 →y=3
→y=3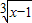 +1;y=
+1;y= →y=
→y=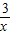 +1;…
+1;…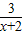 +1图象再往 平移 个单位,所得函数图象的解析式为y=
+1图象再往 平移 个单位,所得函数图象的解析式为y=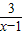 +1;
+1; +1图象性质的描述:
+1图象性质的描述:科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
科目:czsx 来源:活学巧练 九年级数学 下 题型:044
已知抛物线y=ax2+c的顶点为D(0,![]() ),且过点A(1,
),且过点A(1,![]() ),如图所示.
),如图所示.
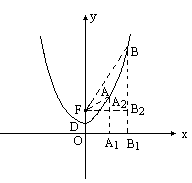
(1)试求这条抛物线的代数表达式;
(2)点F是坐标原点O关于该抛物线顶点D的对称点,坐标为(0,![]() ),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=
),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=![]() -
-![]() =
=![]() .在Rt△AFA2中,有FA=
.在Rt△AFA2中,有FA=![]() =
=![]() .
.
已知抛物线上另一点B的横坐标为2,求线段FB的长.
(3)若点P是该抛物线上在第一象限内的任意一点,试探究线段FP的长度与点P的纵坐标的大小关系,并证明你的猜想.
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2010年辽宁省盘锦市中考数学试卷(解析版) 题型:解答题
科目:czsx 来源:2010年浙江省杭州市萧山区临浦片九年级(下)期初数学试卷(解析版) 题型:填空题
 →y=3
→y=3 +1;y=3
+1;y=3 →y=3
→y=3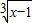 +1;y=
+1;y=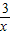 →y=
→y=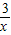 +1;…
+1;…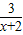 +1图象再往 平移 个单位,所得函数图象的解析式为y=
+1图象再往 平移 个单位,所得函数图象的解析式为y= +1;
+1;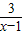 +1图象性质的描述:
+1图象性质的描述:科目:czsx 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:013
反比例函数y=![]() (k≠0)任取一点M(a,b),过M作MA⊥x轴,MB⊥y轴,所得矩形OAMB的面积为S=MA·MB=|b|·|a|=|ab|.又因为b=
(k≠0)任取一点M(a,b),过M作MA⊥x轴,MB⊥y轴,所得矩形OAMB的面积为S=MA·MB=|b|·|a|=|ab|.又因为b=![]() ,故ab=k,所以S=|k|(如图(1)).
,故ab=k,所以S=|k|(如图(1)).
这就是说,过双曲线上任意一点作x轴、y轴的垂线,所得的矩形面积为|k|.这就是k的几何意义,会给解题带来方便.现举例如下:
例1:如(2)图,已知点P1(x1,y1)和P2(x2,y2)都在反比例函数y=![]() (k<0)的图像上,试比较矩形P1AOB与矩形P2COD的面积大小.
(k<0)的图像上,试比较矩形P1AOB与矩形P2COD的面积大小.
解答:![]() =|k|
=|k|
![]() =|k|
=|k|
故![]() =
=![]()
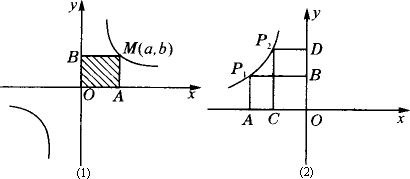
例2:如图(3),在y=![]() (x>0)的图像上有三点A、B、C,经过三点分别向x轴引垂线,交x轴于A1、B1、C1三点,连结OA、OB、OC,记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3,则有( )
(x>0)的图像上有三点A、B、C,经过三点分别向x轴引垂线,交x轴于A1、B1、C1三点,连结OA、OB、OC,记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3,则有( )
A.S1=S2=S3
B.S1<S2<S3
C.S3<S1<S2
D.S1>S2>S3
解答:∵![]() =
=![]() |k|=
|k|=![]() ,
,
![]() =
=![]() |k|=
|k|=![]()
![]() =
=![]() |k|=
|k|=![]()
S1=S2=S3,故选A.
例3:一个反比例函数在第三象限的图像如图(4)所示,若A是图像任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,那么这个反比例函数的解析式是________.
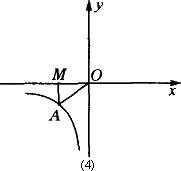
解答:∵S△AOM=![]() |k|
|k|
又S△AOM=3,
∴![]() |k|=3,|k|=6
|k|=3,|k|=6
∴k=±6
又∵曲线在第三象限
∴k>0∴k=6
∴所以反比例函数的解析式为y=![]() .
.
根据是述意义,请你解答下题:
如图(5),过反比例函数y=![]() (x>0)的图像上任意两点A、B分别作轴和垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得
(x>0)的图像上任意两点A、B分别作轴和垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得
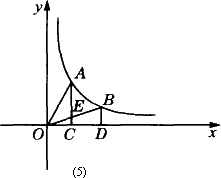
A.S1>S2
B.S1=S2
C.S1<S2
D.大小关系不能确定