科目：gzsx 来源： 题型：填空题
科目：gzsx 来源：2015届苏教版选修2-3高二数学双基达标2.1练习卷（解析版） 题型：解答题
设随机变量X的分布列为P(X＝i)＝
，(i＝1,2,3,4)．
(1)求P(X＜3)；
(2)求P
；
(3)求函数F(x)＝P(X＜x)．
科目：gzsx 来源： 题型：
(i=1,2，3,4)，求：(1)P(X=1或X=2)；(2)P(
＜X＜
)；
(3)函数F(x)=P(X＜x)，若P(X＜x)=
，求x的最大值.
科目：gzsx 来源： 题型：选择题
| A． | 0≤f（x）≤1 | B． | P{X=x}=f（x） | C． | P{X=x}=F（x） | D． | P{X≤x}=F（x） |
科目：gzsx 来源： 题型：解答题
科目：gzsx 来源：2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷（解析版） 题型：填空题
某随机变量X服从正态分布，其概率密度函数为
，则X的期望
，标准差
。
科目：gzsx 来源： 题型：
| ξ | 0 | 1 | 2 |
| P | a | b | c |
A、
| ||
B、
| ||
C、
| ||
D、
|
科目：gzsx 来源： 题型：选择题
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
科目：gzsx 来源： 题型：
| 2 |
| 3 |
科目：gzsx 来源： 题型：
下列4个命题：
①
；
②已知随机变量X服从正态分布N（3，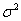
），P（X≤6）=0．72，则P（X≤0）=0．28;
③函数
为奇函数的充要条件是
；
④已知
则
方向上的投影为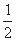
，
其中正确命题的序号是 .
科目：gzsx 来源：不详 题型：单选题
| 1 | ||
|
| x2 |
| 8 |
| A．0和8 | B．0和4 | C．0和
| D．0和2 |
科目：gzsx 来源：设计必修一数学(人教A版) 人教A版 题型：044
17世纪，科学家们致力于运动的研究，如计算天体的位置，远距离航海中对经度和纬度的测量，炮弹的速度对于高度和射程的影响等．诸如此类的问题都需要探究两个变量之间的关系，并根据这种关系对事物的变化规律作出判断，如根据炮弹的速度推测它能达到的高度和射程．这正是函数产生和发展的背景．
“function”一词最初由德国数学家莱布尼兹(G．W．Leibniz，1646～1716)在1692年使用．在中国，清代数学家李善兰(1811～1882)在1859年和英国传教士伟烈亚力合译的《代徽积拾级》中首次将“function”译做“函数”．
莱布尼兹用“函数”表示随曲线的变化而改变的几何量，如坐标、切线等．1718年，他的学生，瑞士数学家约翰·伯努利(J．Bernoulli，1667～1748)强调函数要用公式表示．后来，数学家认为这不是判断函数的标准．只要一些变量变化，另一些变量随之变化就可以了．所以，1755年，瑞士数学家欧拉(L．Euler，1707～1783)将函数定义为“如果某些变量，以一种方式依赖于另一些变量，我们将前面的变量称为后面变量的函数”．
当时很多数学家对于不用公式表示函数很不习惯，甚至抱怀疑态度．函数的概念仍然是比较模糊的．
随着对微积分研究的深入，18世纪末19世纪初，人们对函数的认识向前推进了．德国数学家狄利克雷(P．G．L．Dirichlet，1805～1859)在1837年时提出：“如果对于x的每一个值，y总有一个完全确定的值与之对应，则y是x的函数”．这个定义较清楚地说明了函数的内涵．只要有一个法则，使得取值范围中的每一个值，有一个确定的y和它对应就行了，不管这个法则是公式、图象、表格还是其他形式．19世纪70年代以后，随着集合概念的出现，函数概念又进而用更加严谨的集合和对应语言表述，这就是本节学习的函数概念．
综上所述可知，函数概念的发展与生产、生活以及科学技术的实际需要紧密相关，而且随着研究的深入，函数概念不断得到严谨化、精确化的表达，这与我们学习函数的过程是一样的．
你能以函数概念的发展为背景，谈谈从初中到高中学习函数概念的体会吗？
1．探寻科学家发现问题的过程，对指导我们的学习有什么现实意义？
2．莱布尼兹、狄利克雷等科学家有哪些品质值得我们学习？
，(i＝1,2,3,4)．
；
，(i＝1,2,3,4)．
；