
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:阅读理解
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| PQ |
| 1 |
| PR |
科目:czsx 来源: 题型:解答题

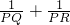 的值;
的值;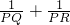 的值;
的值; 的值,并给出证明.
的值,并给出证明.科目:czsx 来源:北京模拟题 题型:解答题
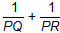 的值;
的值;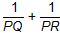 的值;
的值;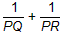 的值,并给出证明。
的值,并给出证明。科目:czsx 来源:2010-2011学年北京市人大附中九年级(上)数学统练试卷(2)(解析版) 题型:解答题
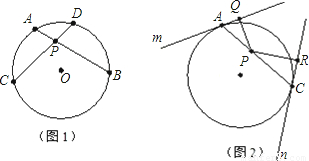
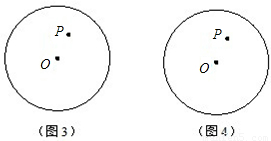
 的值;
的值; 的值;
的值; 的值,并给出证明.
的值,并给出证明.科目:czsx 来源: 题型:解答题
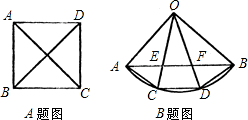
科目:czsx 来源:潍坊 题型:解答题
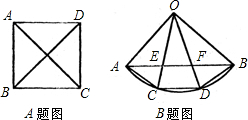
科目:czsx 来源:2003年山东省潍坊市中考数学试卷(解析版) 题型:解答题
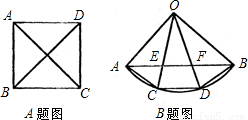
科目:czsx 来源: 题型:
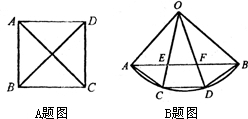
科目:czsx 来源:2009年北京市东城区中考数学一模试卷(解析版) 题型:解答题
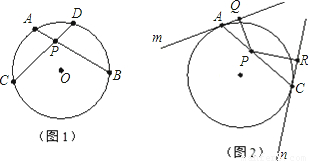
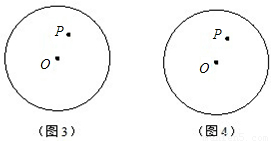
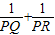 的值;
的值; 的值;
的值;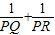 的值,并给出证明.
的值,并给出证明.科目:czsx 来源: 题型:
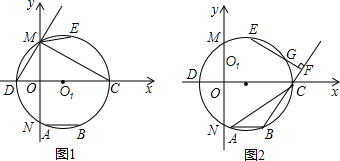
 如图,直线AB经过⊙O的圆心O,且与⊙O交于A、B两点,AB=4,半径OC的延长线与过点B的直线交于点D,OC=CD,BC=
如图,直线AB经过⊙O的圆心O,且与⊙O交于A、B两点,AB=4,半径OC的延长线与过点B的直线交于点D,OC=CD,BC=| 1 | 2 |
科目:gzsx 来源:江苏省启东中学2012届高三上学期期中考试数学试题(物理班) 题型:047
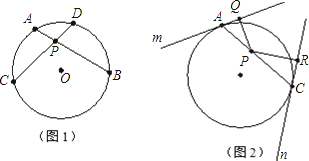
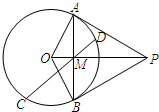
如图,从圆O外一点P作圆O的两条切线,切点分别为A,B,AB与OP交于点M,设CD为过点M且不过圆心O的一条弦,求证:O、C、P、D四点共圆.

科目:czsx 来源: 题型:解答题
 如图,直线AB经过⊙O的圆心O,且与⊙O交于A、B两点,AB=4,半径OC的延长线与过点B的直线交于点D,OC=CD,BC=
如图,直线AB经过⊙O的圆心O,且与⊙O交于A、B两点,AB=4,半径OC的延长线与过点B的直线交于点D,OC=CD,BC= OD.点Q为⊙O上一动点.
OD.点Q为⊙O上一动点.科目:czsx 来源:2008-2009学年九年级数学元月调考模拟试卷(2)(解析版) 题型:解答题
 OD.点Q为⊙O上一动点.
OD.点Q为⊙O上一动点.
科目:czsx 来源:不详 题型:解答题
| 1 |
| 2 |

科目:gzsx 来源: 题型:解答题
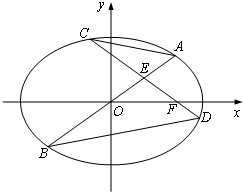 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆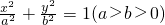 的右焦点为F(1,0),离心率为
的右焦点为F(1,0),离心率为 .分别过O,F的两条弦AB,CD相交于点E(异于A,C两点),且OE=EF.
.分别过O,F的两条弦AB,CD相交于点E(异于A,C两点),且OE=EF.科目:gzsx 来源: 题型:
 (2013•南通三模)如图,在平面直角坐标系xOy中,椭圆
(2013•南通三模)如图,在平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
科目:gzsx 来源: 题型:
 附加题 选做题在A、B、C、D四小题中只能选做两小题,每小题10分,共计20分,解答时应写出文字说明、证明过程或演算步骤.
附加题 选做题在A、B、C、D四小题中只能选做两小题,每小题10分,共计20分,解答时应写出文字说明、证明过程或演算步骤.