正方形ABCD答案解析

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

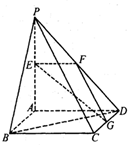如图，P为正方形ABCD所在平面外一点PA⊥平面ABCD，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
（I）求证：EF∥平面ABCD；
（II）求证：平面PBC∥平面EFG；
（III）求异面直线EG与BD所成角的大小．

科目：gzsx 来源： 题型：

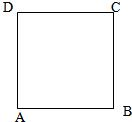
（2011•揭阳一模）如图①边长为1的正方形ABCD中，点E、F分别为AB、BC的中点，将△BEF剪去，将△AED、△DCF分别沿DE、DF折起，使A、C两点重合于点P得一三棱锥如图②示．
（1）求证：PD⊥EF；
（2）求三棱锥P-DEF的体积；
（3）求点E到平面PDF的距离．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

P是边长为4的正方形ABCD所在平面外一点，AP=2，且AP与平面ABCD成45°角，则CP的最小值为

2

5

2

5

．

科目：gzsx 来源： 题型：

在边长为2的正方形ABCD的边上有动点M，从点B开始，沿折线BCDA向A点运动，设M点运动的距离为x，△ABM的面积为S．
（1）求函数S=f（x）的解析式、定义域和值域；
（2）求f[f（3）]的值．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

（2012•江苏二模）如图，已知正方形ABCD和直角梯形BDEF所在平面互相垂直，BF⊥BD，EF=BF=

1

2

BD．
（1）求证：DE∥平面ACF；
（2）求证：BE⊥平面ACF．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C-ABD，它的主视图与俯视图如图所示，则异面直线AB与CD所成角为

60°

60°

．

科目：gzsx 来源： 题型：

两个边长均为3的正方形ABCD和ABEF所在平面垂直相交于AB，M∈AC，N∈FB，且AM=FN．
（1）证明：MN∥平面BCE；
（2）当AM=FN=

2

  时，求MN的长度．

科目：gzsx 来源： 题型：

19、P为正方形ABCD所在平面外一点，PA⊥面ABCD，AE⊥PB，求证：AE⊥PC．

科目：gzsx 来源： 题型：

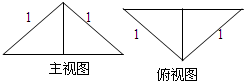把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥C-ABD的主视图与俯视图如图所示，则左视图的面积为（　　）

A、 2 2

B、 1 2

C、 2 4

D、 1 4

科目：gzsx 来源： 题型：

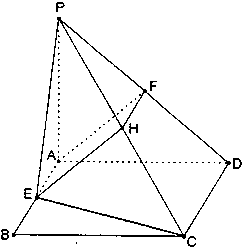（2004•朝阳区一模）如图，已知PA垂直于正方形ABCD所在的平面，E、F分别为AB、PD的中点，过AE、AF的平面交PC于点H，二面角P-CD-B为45°，PA=a．
（Ⅰ）求证：AF∥EH；
（Ⅱ）求证：平面PCE⊥平面PCD； 
（Ⅲ）求多面体ECDAHF的体积．

科目：gzsx 来源： 题型：

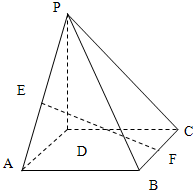已知四棱锥P-ABCD中，PD⊥平面ABCD，正方形ABCD边长为2，PD=2，E，F分别是PA、BC的中点
（1）求证：EF∥平面PDC；
（2）求证：DE⊥PB．