当n=120答案解析

科目：czsx 来源： 题型：

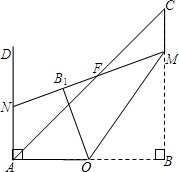（2012•虹口区二模）如图，△ABC中，∠ABC=90°，AB=BC=4，点O为AB边的中点，点M是BC边上一动点（不与点B、C重合），AD⊥AB，垂足为点A．连接MO，将△BOM沿直线MO翻折，点B落在点B₁处，直线M B₁与AC、AD分别交于点F、N．
（1）当∠CMF=120°时，求BM的长；
（2）设BM=x，y=

△CMF的周长

△ANF的周长

，求y关于x的函数关系式，并写出自变量x的取值范围；
（3）连接NO，与AC边交于点E，当△FMC和△AEO相似时，求BM的长．

科目：czsx 来源： 题型：

（2013•梅列区模拟）已知：∠DBC=∠ACB，BC=2AC，BD=BC，CD、AB交于点E．
（1）如图①，当∠ACB=90°时，求出线段DE、CE之间的数量关系；
（2）如图②，当∠ACB=120°时，求证：DE=3CE；
（3）如图③，在（2）的条件下，F是BC边的中点，连接DF交AB于点G，若CE=2，求DF的长．

科目：czsx 来源： 题型：

已知：在△ABC中，BC=2AC，∠DBC=∠ACB，BD=BC，CD交线段AB于点E．
（1）如图1，当∠ACB=90°时，则线段DE、CE之间的数量关系为

 

；
（2）如图2，当∠ACB=120°时，求证：DE=3CE；
（3）如图3，在（2）的条件下，点F是BC边的中点，连接DF，DF与AB交于G，△DKG和△DBG关于直线DG对称（点B的对称点是点K，延长DK交AB于点H．若BH=10，求CE的长．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

已知△ABC中，AB=AC，D、E是BC边上的点，将△ABD绕点A旋转，得到△ACD′，连接D′E．
（1）如图1，当∠BAC=120°，∠DAE=60°时，求证：DE=D′E；
（2）如图2，当DE=D′E时，∠DAE与∠BAC有怎样的数量关系？请写出，并说明理由．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

5、如图所示，已知直线BF、CD相交于点O，∠D=40°，下面判定两条直线平行正确的是（　　）

A、当∠C=40°时，AB∥CD

B、当∠A=40°时，AC∥DE

C、当∠E=120°时，CD∥EF

D、当∠BOC=140°时，BF∥DE

科目：czsx 来源： 题型：

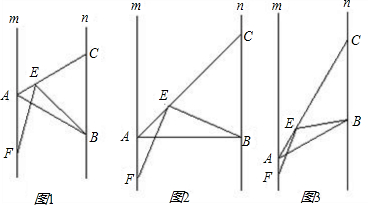
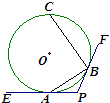已知：如图，在⊙O中，AB是弦，PF切⊙O于点B，直线PE过A点，若PB=PA．
（1）求证：PE是⊙O的切线；
（2）在满足（1）的情况下，当∠APB=120°，B、C分别是⊙O的三等分点，连接BC，且PB=2

3

时，求BC弦的长．

科目：czsx 来源： 题型：

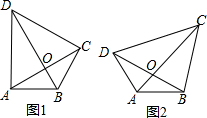在四边形ABCD中，AC、BD相交于点O，∠ABD=∠ACD．
（1）如图1，当∠ABC=120°，∠CBD=60°，AB=BC时，猜想线段AC与CD的数量关系，并加以证明；
（2）如图2，当∠ABC+∠CBD=180°，AB≠BC时，（1）中的结论是否成立，若成立，请加以证明；若不成立，请说明理由．

科目：czsx 来源： 题型：

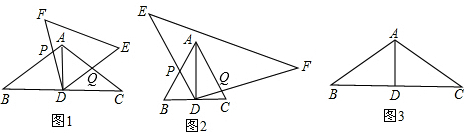
（2010•德州）如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点，交AD于点G，交AB于点F．
（1）求证：BC与⊙O相切；
（2）当∠BAC=120°时，则∠EFG=

30

30

度．

科目：czsx 来源： 题型：

20、如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点，交AD于点G，交AB于点F．（1）求证：BC与⊙O相切；
（2）当∠BAC=120°时，求∠EFG的度数．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

在四边形ABCD中，对角线AC平分∠DAB．

（1）如图①，当∠DAB=120°，∠B=∠D=90°时，求证：AB+AD=AC．
（2）如图②，当∠DAB=120°，∠B与∠D互补时，线段AB、AD、AC有怎样的数量关系？写出你的猜想，并给予证明．
（3）如图③，当∠DAB=90°，∠B与∠D互补时，线段AB、AD、AC有怎样的数量关系？写出你的猜想，并给予证明．

科目：czsx 来源： 题型：

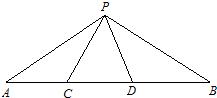23、已知：如图，点C、D在线段AB上．
（1）如果△PCD是等边三角形，当∠APB=

120°

时，△ACP∽△PDB；
（2）如果△PCD是等腰直角三角形，且PC=PD，当∠APB=

135°

时，△ACP∽△PDB；
（3）如果△PCD是等腰三角形，其中PC=PD，∠PCD=30°，试猜想当∠APB等于多少度时，△ACP∽△PDB．请证明你在（3）中的猜想．

科目：czsx 来源： 题型：

已知△ABC中，AB=AC，D、E是BC边上的点，将△ABD绕点A旋转，得到△ACD′，连结D′E．
（1）如图1，当∠BAC=120°，∠DAE=60°时，求证：DE=D′E；
（2）如图2，当DE=D′E时，∠DAE与∠BAC有怎样的数量关系？请写出，并说明理由．
（3）如图3，在（2）的结论下，当∠BAC=90°，BD与DE满足怎样的数量关系时，△D′EC是等腰直角三角形？（直接写出结论，不必说明理由）

科目：czsx 来源： 题型：

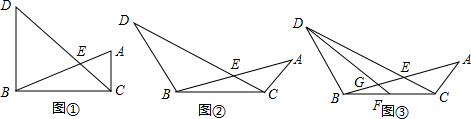
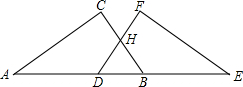已知，如图，点A、D、B、E在同一直线上，AC=EF，AD=BE，∠A=∠E，
（1）求证：△ABC≌△EDF；
（2）当∠CHD=120°，求∠HBD的度数．

科目：czsx 来源： 题型：

如图1，△ABC与△DEF中，AB=AC，D为BC的中点，∠EDF+∠BAC=180°，直线DF、DE分别交直线AB、AC于点P、Q．
（1）如图2，∠BAC=60°，猜想BP+QC与BC的关系，并说明理由；
（2）当∠BAC=120°，BP+QC与BC的关系为

 

；
（3）当∠BAC=α，探究BP+QC与BC的关系，并说明理由；
（4）如图3，当△DEF绕点D旋转时，其他条件不变，（3）中的结论是否一定成立？若成立，请你写出一个真命题；若不成立，请你画图说明．

科目：czsx 来源： 题型：

如图（1）正方形ABCD和正方形AEFG，边AE在边AB上，AB=12，AE=6

2

．将正方形AEFG绕点A逆时针旋转α（0°≤α≤45°）
（1）如图（2）正方形AEFG旋转到此位置，求证：BE=DG；
（2）在旋转的过程中，当∠BEA=120°时，试求BE的长；
（3）BE的延长线交直线DG于点Q，当正方形AEFG由图（1）绕点A逆时针旋转45°，请直接写出旋转过程中点Q运动的路线长；
（4）在旋转的过程中，是否存在某时刻BF=BC？若存在，试求出DQ的长；若不存在，请说明理由．（点Q即（3）中的点）

科目：czsx 来源： 题型：

已知：点A、B分别是直线m、n上两点，在直线n上找一点C，使BC=AB，连接AC，在线段AC上取一点E，作∠BEF=∠ABC，EF交直线m于点F．
（1）当∠ABC=60°时（如图1），求证：AE+AF=BC；
（2）当∠ABC=90°时（如图2），则AE、AF、BC之间的数量关系是

 

；
（3）当∠ABC=120°时（如图3），设EF与AB交于点M，若AC=4

3

，AF=1，求EM的长．

科目：czsx 来源： 题型：

（2012•南岗区一模）已知：菱形ABCD中，BD为对角线，|P、Q两点分别在AB、BD上，且满足∠PCQ=∠ABD，
（1）如图1，当∠BAD=90°时，证明：

2

DQ+BP=CD；
（2）如图2，当∠BAD=120°时，则

3

3

DQ+BP=

2

2

CD；    
（3）如图3，在（2）的条件下，延长CQ交AD边点E，交BA延长线于M，作∠DCE的平分AD边于F若CQ：PM=5：7，EF=

35

24

，求线段BP的长．