
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| lnx+k | ex |
科目:gzsx 来源:无为县模拟 题型:填空题
| x |
| 1+|x| |
科目:gzsx 来源: 题型:
| 5 |
| ||
| 2 |
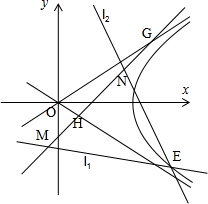
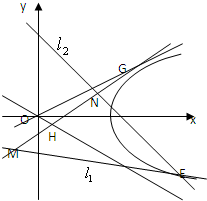
科目:gzsx 来源: 题型:
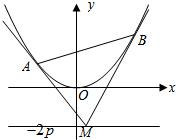 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.| 10 |
| OC |
| OA |
| OB |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 3 | 2 |
科目:gzsx 来源: 题型:
| 1 |
| a-2 |
| 1 |
| 2 |
| 1 |
| 16 |
| A、M>N | B、M=N |
| C、M<N | D、不能确定 |