练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知0

    已知0答案解析

    科目：gzsx 来源： 题型：

    已知0＜θ＜1800，且θ角的6倍角的终边和θ角终边重合，则满足条件的角θ为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜x＜
    1
    2
    ，函数y=x（1-2x）的最大值是
    1
    8
    1
    8
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•南通一模）已知0＜a＜1，若loga（2x-y+1）＞loga（3y-x+2），且λ＜x+y，则λ的最大值为
    -2
    -2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜α＜
    π
    2
    ，sinα=
    4
    5
    ．
    （1）求
    sin2α+sin2α
    cos2α+cos2α
    的值．
    （2）若0＜β＜
    π
    2
    ，且cos（α+β）=
    5
    13
    ，求cosβ的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜α＜
    π
    4
    ，设x=（sinα）sinα，y=（cosα）sinα，z=（sinα）cosα，则（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0≤x≤
    π2
    ，求函数y=cos2x-2acosx的最大值M（a）与最小值m（a）．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜a＜
    π
    2
    ，0＜β＜
    π
    2
    ，且cos(a+
    π
    3
    )=
    5
    13
    ，sin(β-
    π
    3
    )=-
    3
    5
    ，则cos（a+β）的值为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜α＜
    π
    2
    ，tan
    α
    2
    =
    1
    2
    ，求值：（1）tanα（2）cos（α-
    π
    3
    ）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知α∈(0，
    π
    2
    )，cosα=
    1
    3
    ，则sinα=
    2
    		2
    3
    2
    		2
    3
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知α∈(0，
    π
    2
    )    ，tanα=
    1
    2
    ，求
    （1）tan2α
    （2）sin(2α+
    π
    3
    )    的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f(x)=
    		2
    +2
    		6
    sinxcosx-2
    		2
    sin2x，(x∈R)
    （I）对f（x）的图象作如下变换：先将f（x）的图象向右平移
    π
    12
    个单位，再将横坐标伸长到原来的2倍，纵坐标不变，得到函数g（x）的图象，求g（x）的解析式；
    （II）已知0＜x1＜
    π
    2
    ＜x2＜π    ，且g(x1)=
    6
    		2
    5
    ，g(x2)=2    ，求tan（x1+x2）的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

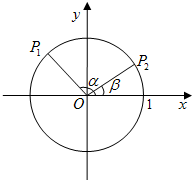    （1）如图，已知α、β是坐标平面内的任意两个角，且0≤α-β≤π，证明两角差的余弦公式：cos（α-β）=cosαcosβ+sinαsinβ；
    （2）已知α∈(0，
    π
    2
    )，β∈(
    π
    2
    ，π)    ，且cosβ=-
    1
    3
    ，sin(α+β)=
    7
    9
    ，求2cos2α+cos2α的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜α＜
    π
    2
    ，且cosα=
    4
    5
    ，则tan(α+
    π
    4
    )    等于（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜m＜a＜b，若x=sin
    a-m
    b-m
    ，y=sin
    a
    b
    ，z=sin
    a+m
    b+m
    则（　　）
    A、x＞y＞z
    B、x＜y＜z
    C、x＜y且y＜z
    D、x＞y且z＞y

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜α＜
    π
    2
    ，π＜β＜
    3π
    2
    ，且tanα=
    1
    3
    ，cosβ=-
    		5
    5
    ，则β-α=
    5π
    4
    5π
    4
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•自贡一模）已知α∈(0，
    π
    2
    )且sinα=
    3
    5
    ，则
    		2
    sin(α-
    π
    4
    )    =（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0≤a≤10（a为常数），在区间[0，10]上任取两个实数x，y，设“2x+y≤a”的概率为p，“x-2y≥a”的概率为q，若有p≤q，则实数a的取值范围
    {0，5]
    {0，5]
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•唐山一模）已知α∈(0，π)，cos(α+
    π
    6
    )=
    		2
    2
    ，则 tan2α=（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=x2-（c+1）x+c（c∈R）．
    （1）解关于x的不等式f（x）＜0；
    （2）当c=-2时，不等式f（x）＞ax-5在（0，2）上恒成立，求实数a的取值范围；
    （3）设g（x）=f（x）-ax，已知0＜g（2）＜1，3＜g（3）＜5，求g（4）的范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知0＜x＜1，则函数y=
    		x(1-x)
    的最大值等于
    1
    2
    1
    2
    ．

    查看答案和解析>>