
科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,⊙C与x轴相切于D点,与y轴相交于A(0,2)、B(0,8)两点,圆心C在第一象限.
如图,在平面直角坐标系中,⊙C与x轴相切于D点,与y轴相交于A(0,2)、B(0,8)两点,圆心C在第一象限.科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,抛物线与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,4),顶点为(1,5).
如图,在平面直角坐标系中,抛物线与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,4),顶点为(1,5).科目:czsx 来源: 题型:
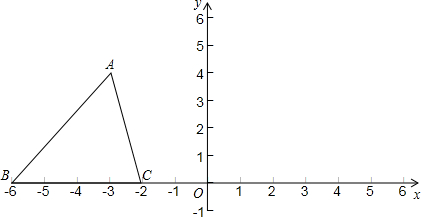

科目:czsx 来源:2011年福建省龙岩市连城一中自主招生考试数学试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线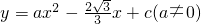 经过A、B、C三点.
经过A、B、C三点.科目:czsx 来源:2011-2012学年浙江省丽水市缙云县中考模拟数学试卷(解析版) 题型:解答题
已知在平面直角坐标系中,直线 与x轴,y轴相交于A,B两点,
 直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
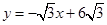
 动到点A,过点D作x轴的垂线,分别交直线
和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
动到点A,过点D作x轴的垂线,分别交直线
和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
 (1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值;
(1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值;
(3)求S关于t的函数关系式,并写出相应t的取值范围,
求出D在整个运动过程中s的最大值。

科目:czsx 来源: 题型:解答题
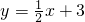 与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.
与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.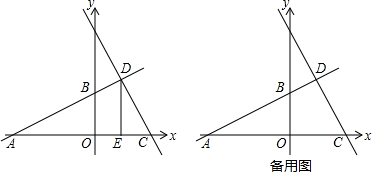
科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,4),顶点为(1,5).
如图,在平面直角坐标系中,抛物线与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,4),顶点为(1,5).科目:czsx 来源:2013年四川省泸州市天立学校中考数学一模试卷(解析版) 题型:解答题
 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线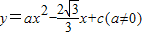 经过A、B、C三点.
经过A、B、C三点.
科目:czsx 来源:2011-2012学年江苏省苏州市常熟市九年级(上)期末数学试卷(解析版) 题型:解答题

科目:czsx 来源:2012年黑龙江省哈尔滨市中考调研测试数学试卷(解析版) 题型:解答题
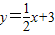 与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.
与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.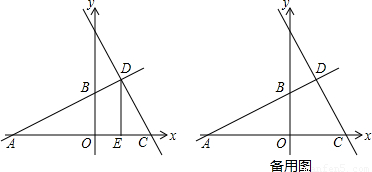
科目:czsx 来源:2012届浙江省丽水市缙云县中考模拟数学试卷(带解析) 题型:解答题
已知在平面直角坐标系中,直线 与x轴,y轴相交于A,B两点, 直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
 动到点A,过点D作x轴的垂线,分别交直线 和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
动到点A,过点D作x轴的垂线,分别交直线 和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒) (1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值;
(1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值;
(3)求S关于t的函数关系式,并写出相应t的取值范围,
求出D在整个运动过程中s的最大值。
科目:czsx 来源:2012年浙江省金华市中考数学模拟试卷(三)(解析版) 题型:解答题
 与x轴,y轴相交于A,B两点,直线
与x轴,y轴相交于A,B两点,直线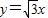 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线 和直线
和直线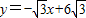 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)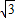 )正好在△PQR的某边上,求t的值;
)正好在△PQR的某边上,求t的值;
科目:czsx 来源: 题型:解答题
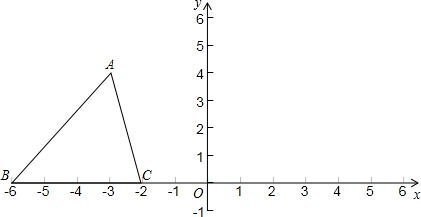
科目:czsx 来源:2012年中考数学模拟重点试题卷(一)(解析版) 题型:解答题
 与x轴,y轴相交于A,B两点,直线
与x轴,y轴相交于A,B两点,直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线 和直线
和直线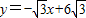 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒) )正好在△PQR的某边上,求t的值;
)正好在△PQR的某边上,求t的值;
科目:czsx 来源:2011年浙江省金华市金东区中考数学模拟试卷(5月份)(解析版) 题型:解答题
 与x轴,y轴相交于A,B两点,直线
与x轴,y轴相交于A,B两点,直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线 和直线
和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒) )正好在△PQR的某边上,求t的值;
)正好在△PQR的某边上,求t的值;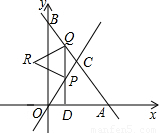
科目:czsx 来源:2012年浙江省丽水市缙云县中考数学模拟试卷(解析版) 题型:解答题
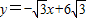 与x轴,y轴相交于A,B两点,直线
与x轴,y轴相交于A,B两点,直线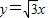 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线 和直线
和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)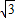 )正好在△PQR的某边上,求t的值;
)正好在△PQR的某边上,求t的值;
科目:czsx 来源: 题型:
 10、如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),则点Q的坐标是( )
10、如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),则点Q的坐标是( )科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,⊙M与x轴交于A,B两点,AC是⊙M的直径,过点C的直线交x轴于点D,连接BC,已知点M的坐标为(0,
如图,在平面直角坐标系中,⊙M与x轴交于A,B两点,AC是⊙M的直径,过点C的直线交x轴于点D,连接BC,已知点M的坐标为(0,| 3 |
| 3 |
| 3 |