如图，点A, B ,C在圆心O上，点D在圆心O内，点A与点D在点B,C所在直线的同侧，答案解析

科目：czsx 来源： 题型：

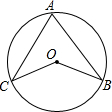
（2013•泰安）如图，点A，B，C，在⊙O上，∠ABO=32°，∠ACO=38°，则∠BOC等于（　　）

A．60°

B．70°

C．120°

D．140°

科目：czsx 来源： 题型：

如图：人民海关缉私巡逻艇在东海执行巡逻任务时，发现在其所在位置O点的北偏西30°方向40海里的A点有一走私船正向正东方向航行，1小时后，测得走私船在O点的北偏东30°方向的B点．
（1）求走私船的速度；
（2）若走私船以同样的速度继续向正东方向航行，而巡逻艇在发现走私船在B点时，即刻沿北偏东45°方向以50海里/小时的速度追赶，问能否追上走私艇？
（3）若巡逻艇在发现走私船在B点时，即刻沿北偏东60°方向航行并追上走私船，问巡逻艇的航行速度至少达到多少海里/小时？

科目：czsx 来源： 题型：

19、如图，点E、F在△ABC的边上，连接EF，若∠B=50°，则∠1+∠2+∠3+∠4的度数为

260°

．

科目：czsx 来源： 题型：

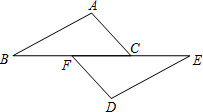
（2011•郑州模拟）已知命题：“如图，点B、F、C、E在同一条直线上，则AB∥DE．”判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，在不添加其他辅助线的情况下，请添加一个适当的条件使它成为真命题，并加以证明．

科目：czsx 来源： 题型：

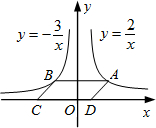
（2012•荆州）如图，点A是反比例函数y=

2

x

（x＞0）的图象上任意一点，AB∥x轴交反比例函数y=-

3

x

的图象于点B，以AB为边作▱ABCD，其中C、D在x轴上，则S_□ABCD为（　　）

A．2

B．3

C．4

D．5

科目：czsx 来源： 题型：

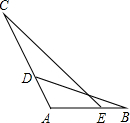
（2012•浦东新区二模）已知：如图，点D、E分别在线段AC、AB上，AD•AC=AE•AB．
（1）求证：△AEC∽△ADB；
（2）AB=4，DB=5，sinC=

1

3

，求S_△ABD．

科目：czsx 来源： 题型：

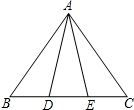
如图，点D，E在△ABC的边BC上，连接AD，AE．①AB=AC；②AD=AE；③BD=CE．以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②⇒③：①③⇒②；②③⇒①
（1）以上三个命题是真命题的为

 

（直接作答）；
（2）请选择一个真命题进行证明（先写出所选命题，然后证明）．

科目：czsx 来源： 题型：

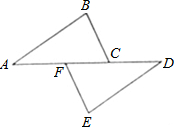
19、如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．求证：BC∥EF．

科目：czsx 来源： 题型：

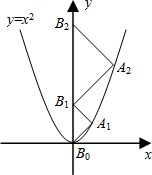
如图，点A₁、A₂、A₃、…、An在抛物线y=x²图象上，点B₁、B₂、B₃、…、B_n在y轴上，若△A₁B₀B₁、△A₂B₁B₂、…、△A_nB_n-1B_n都为等腰直角三角形（点B₀是坐标原点），则△A₂₀₁₁B₂₀₁₀B₂₀₁₁的腰长=

 

．

科目：czsx 来源： 题型：

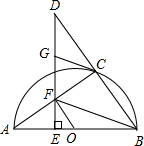
（2012•莆田）如图，点C在以AB为直径的半圆O上，延长BC到点D，使得CD=BC，过点D作DE⊥AB于点E，交AC于点F，点G为DF的中点，连接CG、OF、FB．
（1）求证：CG是⊙O的切线；
（2）若△AFB的面积是△DCG的面积的2倍，求证：OF∥BC．

科目：czsx 来源： 题型：

（2013•萧山区模拟）如图，点P是双曲线y=

4 3

x

（x＞0）上动点，在y轴上取点Q，使得以P、Q、O 为顶点的三角形是含有30°角的直角三角形，则符合条件的点Q的坐标是

（0，2

3

）、（0，2）、（0，

8 3

3

）、（0，8）

（0，2

3

）、（0，2）、（0，

8 3

3

）、（0，8）

．

科目：czsx 来源： 题型：

如图，两块三角板摆放在一起，射线OM平分∠BOC、ON平分∠AOC．
（1）求∠MON的度数；
（2）如果（1）中，一个三角板绕点O旋转一定角度，使得∠AOC=20°，其它条件不变，求∠MON的度数；
（3）如果（1）中，一个三角板绕点O旋转一定角度，使得∠AOC=α，（ α为锐角 ），其它条件不变，求∠MON的度数；
（4）如果（1）中，一个三角板绕点O旋转一定角度，使得∠AOB=β （ β为锐角 ），其它条件不变，求∠MON的度数．

科目：czsx 来源： 题型：

如图，抛物线y=

2

3

x2+

2

3

3

x+c经过x轴上的两点A（x₁，0）、B（x₂，0）和y轴上的点C（0，-

3

2

），⊙P的圆心P在y轴上，且经过B、C两点．
（1）求抛物线的解析式；
（2）D在抛物线上，且C、D两点关于抛物线的对称轴对称，问直线BD是否经过圆心P？并说明理由；
（3）设直线BD交⊙P于另一点E，求经过点E和⊙P的切线的解析式．

科目：czsx 来源： 题型：

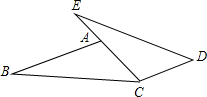
（2012•北京）已知：如图，点E，A，C在同一直线上，AB∥CD，AB=CE，AC=CD．
求证：BC=ED．

科目：czsx 来源： 题型：

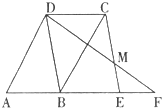
30、如图，点E、F在▱ABCD的边AB的延长线上，且BE=AB，BF=BD，连接CE、DF相交于点M，CD与CM是否相等？请说明理由．

科目：czsx 来源： 题型：

14、如图，点A、D在⊙O上，BC是⊙O的直径，若∠D=35°，则∠OAB的度数是

35°

．

科目：czsx 来源： 题型：

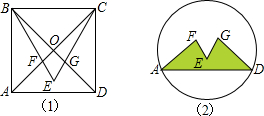
某校开展的一次动漫设计大赛，杨帆同学运用了数学知识进行了富有创意的图案设计，如图（1），他在边长为1的正方形ABCD内作等边△BCE，并与正方形的对角线交于点F、G，制作如图（2）的图标，请我计算一下图案中阴影图形的面积．

科目：czsx 来源： 题型：

21、如图，点A在OC上，点B在OD上，AD与BC相交于点E，若△OAD≌△OBC，且∠O=70°，∠C=25°，则∠AEB等于

120

度．

科目：czsx 来源： 题型：

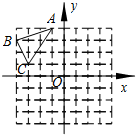
14、如图，△ABC的顶点都在正方形网格格点上，点A的坐标为（-1，4）．将△ABC沿y轴翻折到第一象限，则点C的对应点C′的坐标是

（3，1）

．

科目：czsx 来源： 题型：

如图，点A在反比例函数y=

k

x

的图象上，点B、C分别在x、y轴上，若S_矩形ABOC=4，则k=

 

．