
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
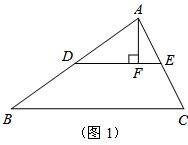 22、小明想把一个三角形拼接成面积与它相等的矩形.他先进行了如下部分操作,如图1所示:
22、小明想把一个三角形拼接成面积与它相等的矩形.他先进行了如下部分操作,如图1所示:
科目:czsx 来源: 题型:
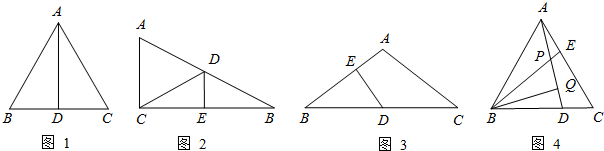
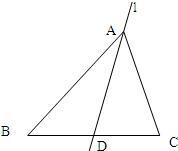 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是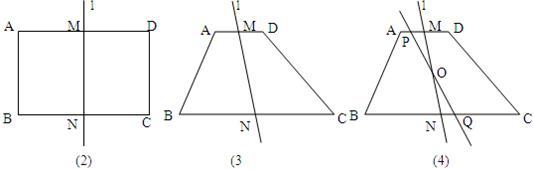
科目:czsx 来源: 题型:阅读理解

科目:czsx 来源: 题型:
 (1)如图1,经历矩形性质的探索过程,你可以发现:直角三角形斜边上的中线等于斜边上的一半.如在Rt△ABC中CD是斜边AB的中线,则CD=
(1)如图1,经历矩形性质的探索过程,你可以发现:直角三角形斜边上的中线等于斜边上的一半.如在Rt△ABC中CD是斜边AB的中线,则CD=| 1 | 2 |
科目:czsx 来源: 题型:
 |
| AB |
 |
| SR |
 |
| TQ |
 |
| QR |
 |
| BC |
 |
| AC |
 |
| AP |
 |
| BP |
| A、1 | B、2 | C、3 | D、4 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |

科目:czsx 来源: 题型:
| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
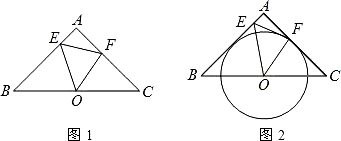
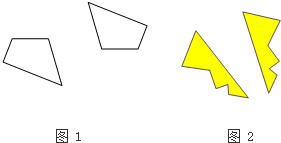 24、(1)如图1中的两个图形成中心对称,找到对称中心O.
24、(1)如图1中的两个图形成中心对称,找到对称中心O.

科目:czsx 来源: 题型:

| 1 | 2 |
科目:czsx 来源: 题型:
(本小题满分5分)
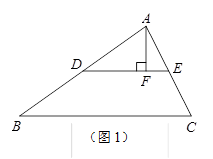
小明想把一个三角形拼接成面积与它相等的矩形.他先进行了如下部分操作,如图1所示:
①取△ABC的边AB、AC的中点D、E,联结DE;
②过点A作AF⊥DE于点F;
(1)请你帮小明完成图1的操作,把△ABC拼接成面积与它相等的矩形.
(2)若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形,那么原三角形的一边与这边上的高之间的数量关系是________________.
(3)在下面所给的网格中画出符合(2)中条件的三角形,并将其拼接成面积与它相等的正方形.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题
 Rt△ABC在直角坐标系内的位置如图1所示,反比例函数
Rt△ABC在直角坐标系内的位置如图1所示,反比例函数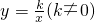 在第一象限内的图象与BC边交于点D(4,m),与直线AB:y=
在第一象限内的图象与BC边交于点D(4,m),与直线AB:y= x+b交于点E(2,n).
x+b交于点E(2,n).科目:czsx 来源: 题型:
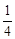 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.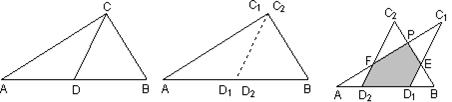
科目:czsx 来源: 题型:


科目:czsx 来源: 题型:
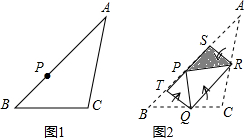
(2011贵州六盘水,25,16分)如图10所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标。
科目:czsx 来源: 题型:
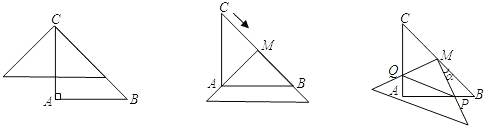
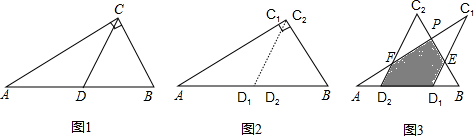
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图2所示).将纸片△AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一直线上),当点D1与点B重合时,停止平移.在平移的过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P.
1.当△AC1D1平移到如图3所示位置时,猜想D1E与D2F的数量关系,并说明理由
2.设平移距离D2D1为x,△AC1D1和△BC2D2重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
3.对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的![]() ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
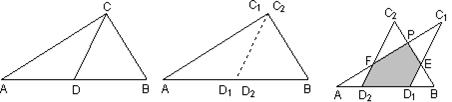
图1 图2 图3