如图,在平面直角坐标系中,点B,C在X轴上,ob》oc答案解析
科目:czsx
来源:
题型:022
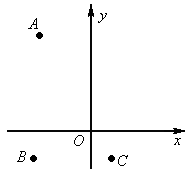
(2005湖北武汉)如图所示平面直角坐标系中,点A、B、C的坐标分别是A(-2,5),B(-3,-1),C(1,-1),在第一象限内找一点D,使四边形ABCD是平行四边形,那么点D的坐标是(____,____).
查看答案和解析>>
科目:czsx
来源:
题型:
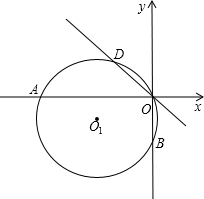
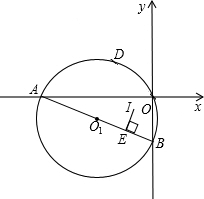
已知,如图:在平面直角坐标系中,点D是直线y=-x上一点,过O、D两点的圆⊙O
1分别交x轴、y轴于点A和B.
(1)当A(-12,0),B(0,-5)时,求O
1的坐标;
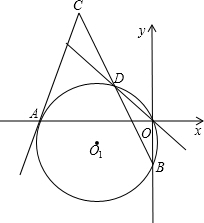
(2)在(1)的条件下,过点A作⊙O
1的切线与BD的延长线相交于点C,求点C的坐标;
(3)若点D的横坐标为
-,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O
1的大小发生变化时,其结论:AE-BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•溧水县一模)七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
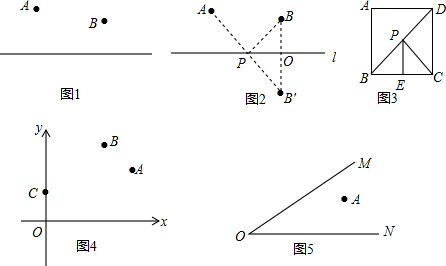
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点就是要求的点P.
有很多问题都可用类似的方法去思考解决.
探究:
(1)如图3,正方形ABCD的边长为2,E为BC的中点,P是BD上一动点.连接EP,CP,则EP+CP的最小值是
;
运用:
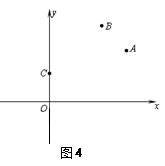
(2)如图4,平面直角坐标系中有三点A(6,4)、B(4,6)、C(0,2),在x轴上找一点D,使得四边形ABCD的周长最小,则点D的坐标应该是
(2,0)
(2,0)
;
操作:
(3)如图5,A是锐角MON内部任意一点,在∠MON的两边OM,ON上各求作一点B,C,组成△ABC,使△ABC周长最小.(不写作法,保留作图痕迹)
查看答案和解析>>
科目:czsx
来源:
题型:
如图,放在平面直角坐标系中的正方形ABCD的边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(如图,它有四个顶点,各顶点数分别是1、2、3、4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点P落在正方形面上(含边界,下同)的概率;
(2)将正方形ABCD平移数个单位,是否存在一种平移,使点P落在正
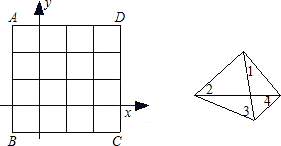
方形面上的概率为
?若存在,指出其中的一种平移方式;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,△ABC是直角三角形,AB为斜边,sin∠BAC=
,现要将它放置在如图2的平面直

角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
(x>0)的图象上.
(1)求k的值和边AC的长;
(2)求点B的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
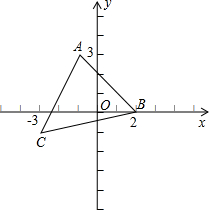
如图已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)
(1)在图中作出△ABC关于y轴的对称图形△A
1B
1C
1,并写出点A
1B
1C
1的坐标.
(2)在y轴上找一点P,使PA+PC最短,并求出P点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
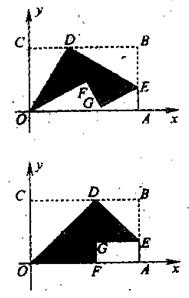
如图1,平面直角坐标系中有一矩形纸片OABC,O为原点,点A、C分别在x轴、y轴上,点B的坐标为(
,1),在BC边上选取适当的点D,将△OCD沿OD翻折,点C落在点E处,得到△OED.
(1)若点E与点A、点B构成等腰三角形,求点E的坐标;
(2)若点E在一次函数y=2x-1的图象上(如图2),求点D的坐标;
(3)当线段OD与直线EA垂直时(如图3),求△CDE的外接圆的半径.

查看答案和解析>>
科目:czsx
来源:
题型:
如图1,平面直角坐标系中,O为坐标原点,直线AB:y=
x+1分别交x、y轴于点A、B,过点A画AC⊥AB,且AC=AB,连接BC得△ABC,将△ABC沿x轴正方向平移后得△A′B′C′.
(1)点B的坐标是
(0,1)
(0,1)
,点C的坐标是
(-3,2)
(-3,2)
(2)平移后当顶点C′正好落在直线AB上,求平移的距离和点B′的坐标;
(3)如图2,将△A′B′C′从(2)的位置开始继续向右平移,连接OB′、OC′,问当点B′在何位置时,△OB′C′的面积是△ABC面积的
倍?请你求出点B′的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:
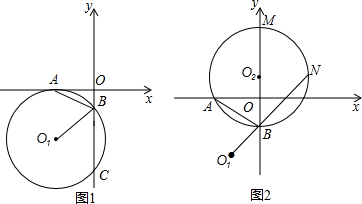
如图1,平面直角坐标系中,⊙O
1与x轴相切于点A,与y轴相交于点B、C两点,连接AB、O
1B.
(1)求证:∠ABO
1=∠ABO;
(2)若点O
1的坐标为(
-,-2),直接写出点B、C的坐标
(3)如图2,在(2)的条件下,过A、B两点作⊙O
2与y轴的正半轴交于点M,与O
1B的延长线交于点N,当⊙O
2的大小变化时,给出下列两个结论:①BM-BN的值不变;②BM+BN的值不变;其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
查看答案和解析>>
科目:czsx
来源:
题型:
已知,如图:在平面直角坐标系中,点D是直线y=-x上一点,过O、D两点的圆⊙O
1分别交X轴、Y轴于点A和B,

(1)当A(-12,0),B(0,-5)时,求O
1的坐标;
(2)在(1)的条件下,过点A作⊙O
1的切线与BD的延长线相交于点C,求点C的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
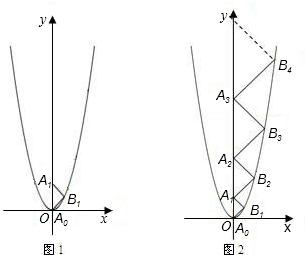
如图1的平面直角坐标系中,等腰直角三角形A
0B
1A
1的斜边A
0A
1落在y轴的正半轴上,A
0A
1=2,点A
0与原点O重合.二次函数y=ax
2的图象恰好经过B
1.
(1)求二次函数的解析式;
(2)在y轴的正半轴依次取点A
2,A
3,A
4,…,A
n,使得以A
1A
2,A
2A
3,A
3A
4,…,A
n-1A
n,为斜边的等腰直角三角形△A
1B
2A
2,△A
2B
3A
3,△A
3B
4A
4,…,△A
n-1B
nA
n的顶点B
2,B
3,B
4,…,B
n分别落在二次函数y=ax
2的图象上(如图2).完成下列填空:A
1A
2=
,A
2A
3=
;
(3)根据(2)观察分析得到的规律,试写出A
n-1A
n的长:A
n-1A
n=
(用n的代数式表示).
查看答案和解析>>
科目:czsx
来源:
题型:
(1)如图1,平面直角坐标系中,已知点A(1,3)和点B(6,2),在x轴上找到一点P,使△ABP的周长最小;并写出点P的坐标.
(2)图2图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象回答下列问题:
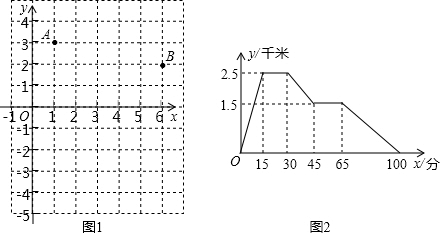
①张强从家到体育场用了
15
15
分钟;
②体育场离文具店
1
1
千米;
③张强在文具店停留了
20
20
分钟;
④张强从文具店回家的平均速度是
千米/分.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•宜昌)如图1,平面直角坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y
1=ax(x-t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y
2=kx(k为常数,k>0)
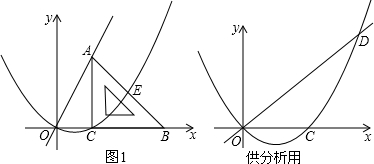
(1)填空:用含t的代数式表示点A的坐标及k的值:A
(t,4)
(t,4)
,k=
;
(2)随着三角板的滑动,当a=
时:
①请你验证:抛物线y
1=ax(x-t)的顶点在函数y=
-x2的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y
2-y
1|的值随x的增大而减小,当x≥t+4时,|y
2-y
1|的值随x的增大而增大,求a与t的关系式及t的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
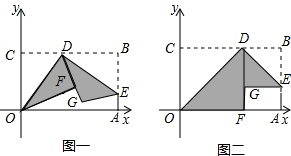
如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.
(1)如图二,若翻折后点F落在OA边上,求直线DE的函数关系式;
(2)设D(a,6),E(10,b),求b关于a的函数关系式,并求b的最小值;
(3)一般地,请你猜想直线DE与抛物线y=-
x
2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x
2+6始终有公共点,请在图一中作出这样的公共点.
查看答案和解析>>
科目:czsx
来源:2012-2013学年湖南长沙周南实验中学八年级上学期段考数学试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,点P 是第一象限直线
是第一象限直线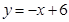 上的点,点A
上的点,点A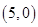 ,O是坐标原点,△PAO的面积为
,O是坐标原点,△PAO的面积为 .
.

⑴求 与
与 的函数关系式,并写出x的取值范围;
的函数关系式,并写出x的取值范围;
⑵探究:当P点运动到什么位置时△PAO的面积为10.
查看答案和解析>>
科目:czsx
来源:2005年江苏省苏州市中考数学试卷(解析版)
题型:解答题
(2005•苏州)如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.
(1)如图二,若翻折后点F落在OA边上,求直线DE的函数关系式;
(2)设D(a,6),E(10,b),求b关于a的函数关系式,并求b的最小值;
(3)一般地,请你猜想直线DE与抛物线y=-

x
2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-

x
2+6始终有公共点,请在图一中作出这样的公共点.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图1的平面直角坐标系中,等腰直角三角形A0B1A1的斜边A0A1落在y轴的正半轴上,A0A1=2,点A0与原点O重合.二次函数y=ax2的图象恰好经过B1.
(1)求二次函数的解析式;
(2)在y轴的正半轴依次取点A2,A3,A4,…,An,使得以A1A2,A2A3,A3A4,…,An-1An,为斜边的等腰直角三角形△A1B2A2,△A2B3A3,△A3B4A4,…,△An-1BnAn的顶点B2,B3,B4,…,Bn分别落在二次函数y=ax2的图象上(如图2).完成下列填空:A1A2=______,A2A3=______;
(3)根据(2)观察分析得到的规律,试写出An-1An的长:An-1An=______(用n的代数式表示).
查看答案和解析>>
科目:czsx
来源:
题型:
七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
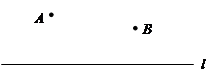

我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
有很多问题都可用类似的方法去思考解决.
探究:
1.如图3,正方形ABCD的边长为2,E为BC的中点, P是BD上一动点.连结EP,CP,则EP+CP的最小值是________;
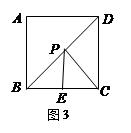
运用:
2.如图4,平面直角坐标系中有三点A(6,4)、B(4,6)、C(0,2),在x轴上找一点D,使得四边形ABCD的周长最小,则点D的坐标应该是 ;
操作:
3.如图5,A是锐角MON内部任意一点,在∠MON的两边OM,ON上各求作一点B,C,组成△ABC,使△ABC周长最小.(不写作法,保留作图痕迹)

查看答案和解析>>
科目:czsx
来源:2012年河南省郑州市中考数学考前五套题(一)(解析版)
题型:解答题
如图1,△ABC是直角三角形,AB为斜边,sin∠BAC=

,现要将它放置在如图2的平面直角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
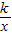
(x>0)的图象上.
(1)求k的值和边AC的长;
(2)求点B的坐标.

查看答案和解析>>
科目:czsx
来源:2005年初中毕业升学考试(江苏苏州卷)数学(带解析)
题型:解答题
查看答案和解析>>






 方形面上的概率为
方形面上的概率为 角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=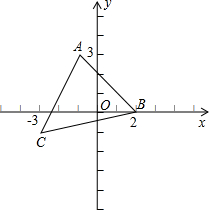 如图已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)
如图已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)






 如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合.
如图一,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B,C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合. 是第一象限直线
是第一象限直线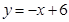 上的点,点A
上的点,点A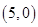 ,O是坐标原点,△PAO的面积为
,O是坐标原点,△PAO的面积为 .
.
 与
与 的函数关系式,并写出x的取值范围;
的函数关系式,并写出x的取值范围; x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=- x2+6始终有公共点,请在图一中作出这样的公共点.
x2+6始终有公共点,请在图一中作出这样的公共点.

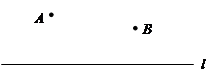

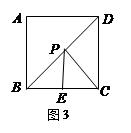


 ,现要将它放置在如图2的平面直角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
,现要将它放置在如图2的平面直角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=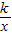 (x>0)的图象上.
(x>0)的图象上.
 的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线 始终有公共点,请在图一中作出这样的公共点。
始终有公共点,请在图一中作出这样的公共点。