如图，已知抛物线y=-1/2x2+（5-）答案解析

科目：czsx 来源：2007中考夺标冲刺模拟题(新课标)(十)、数学 题型：059

如图，已知抛物线y＝2x²－4x＋m与x轴交于不同的两点A、B，其顶点是C，点D是抛物线的对称轴与x轴的交点．

(1)求实数m的取值范围；

(2)求顶点C的坐标和线段AB的长度(用含有m的式子表示)；

(3)若直线分别交x轴、y轴于点E、F，问△BDC与△EOF是否有可能全等，如果可能，请证明；如果不可能，请说明理由．

科目：czsx 来源： 题型：

如图，已知抛物线y=ax²+bx+c（a≠0）过点A（3，0），B（1，0），且与y轴交于点C（0，-3），点P是抛物线AC间上一动点，从点C沿抛物线向点A运动（点P与A、C不重合），过点P作PD∥y轴，交AC于点D．
（1）求该抛物线的函数关系式；
（2）当△ADP是直角三角形时，直接写出点P的坐标；
（3）求线段PD的最大值，并求最大值时P点的坐标；
（4）在问题（3）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

科目：czsx 来源： 题型：

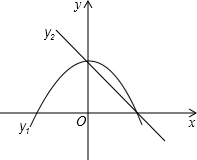（2013•衡水二模）如图，已知抛物线y₁=-x²+1，直线y₂=-x+1，当x任取一值时，x对应的函数值分别为y₁，y₂，若y₁≠y₂，取y₁，y₂中的较小值记为M₁，若y₁=y₂，记M=y₁=y₂，例如：x=2时，y₁=-3，y₂=-1，y₁＜y₂，M=-3．下列判断：
①当x＞0时，y₁＞y₂；
②当x＜0时，x值越大，M值越大；
③使得M大于1的x值不存在；
④使得M=0的x值是1．
其中正确的是（　　）

A．①②

B．①④

C．②③

D．①④

科目：czsx 来源： 题型：

如图，已知抛物线经过坐标原点O及A（-2

3

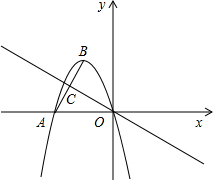，0），其顶点为B（m，3），C是AB中点，点E是直线OC上的一个动点 （点E与点O不重合），点D在y轴上，且EO=ED．
（1）求此抛物线及直线OC的解析式；
（2）当点E运动到抛物线上时，求BD的长；
（3）连接AD，当点E运动到何处时，△AED的面积为

3 3

4

？请直接写出此时E点的坐标．

科目：czsx 来源： 题型：

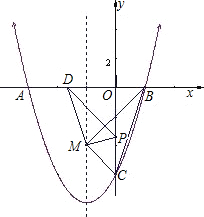如图，已知抛物线y=ax²+bx+c（a≠0）与x轴交于A（-6，0）、B（2，0），与y轴交于点C（0，-6）．
（1）求此抛物线的函数表达式，写出它的对称轴；
（2）若在抛物线的对称轴上存在一点M，使△MBC的周长最小，求点M的坐标；
（3）若点P（0，k）为线段OC上的一个不与端点重合的动点，过点P作PD∥CM交x于点D，连接MD、MP，设△MPD的面积为S，求当点P运动到何处时S的值最大？

科目：czsx 来源： 题型：

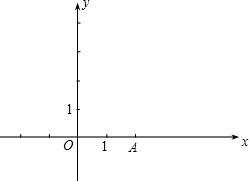如图，已知抛物线 y=-x²+bx+c过点A（2，0），对称轴为y轴，顶点为P．
（1）求该抛物线的表达式，写出其顶点P的坐标，并画出其大致图象；
（2）把该抛物线先向右平移m个单位，再向下平移m个单位（m＞0 ），记新抛物线的顶点为B，与y轴的交点为C．
①试用m的代数式表示点B、点C的坐标；  ②若∠OBC=45°，试求m的值．

科目：czsx 来源： 题型：

如图，已知抛物线y=ax²+bx-3的对称轴为直线x=1，交x轴于A、B两点，交y轴于C点，其中B点的坐标为（3，0）．
（1）直接写出A点的坐标；
（2）求二次函数y=ax²+bx-3的解析式，并求出抛物线的顶点坐标；
（3）在该二次函数的对称轴上是否存在一点P，使得点P到B、C两点的距离相等？若存在，请直接写出P点的坐标；若不存在，请说明理由．

科目：czsx 来源： 题型：

如图，已知抛物线y=ax²+bx+c与x轴交于A、B两点，与y轴交于点C，D为OC的中点，直线AD交抛物线于点E（2，6），且△ABE与△ABC的面积之比为3：2．
（1）求这条抛物线对应的函数关系式；
（2）连接BD，试判断BD与AD的位置关系，并说明理由；
（3）连接BC交直线AD于点M，在直线AD上，是否存在这样的点N（不与点M重合），使得以A、B、N为顶点的三角形与△ABM相似？若存在，请求出点N的坐标；若不存在，请说明理由．

科目：czsx 来源： 题型：

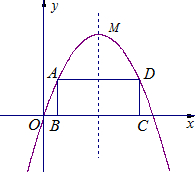如图，已知抛物线y=-x²+bx+9-b²（b为常数）经过坐标原点O，且与x轴交于另一点E．其顶点M在第一象限．
（1）求该抛物线所对应的函数关系式；
（2）设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B，DE⊥x轴于点C．
①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；
②求矩形ABCD的周长的最大值，并写出此时点A的坐标；
③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断并说明理由．

科目：czsx 来源： 题型：

如图，已知抛物线y=a(x-1)2+3

3

(a≠0)经过点A（-2，0），抛物线的顶点为D，过O作射线OM∥AD．过顶点D平行于x轴的直线交射线OM于点C，B在x轴正半轴上，连接BC．
（1）求该抛物线的解析式；
（2）若动点P从点O出发，以每秒l个长度单位的速度沿射线OM运动，设点P运动的时间为t（s）．问：当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？
（3）若OC=OB，动点P和动点Q分别从点O和点B同时出发，分别以每秒l个长度单位和2个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动设它们运动的时间为t（s），连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值．
（4）在（3）中当t为何值时，以O，P，Q为顶点的三角形与△OAD相似？（直接写出答案）

科目：czsx 来源： 题型：

如图，已知抛物线y=mx²+（3-m）x+m²+m交x轴于C（x₁，0），D（x₂，0）两点，（x₁＜x₂）且（x₁+1）（x₂+1）=5
（1）试确定m的值；
（2）过点A（-1，-5）和抛物线的顶点M的直线交x轴于点B，求B点的坐标；
（3）设点P（a，b）是抛物线上点C到点M之间的一个动点（含C、M点），△POQ是以PO为腰、底边OQ在x轴上的等腰三角形，过点Q作x轴的垂线交直线AM于点R，连接PR．设△PQR的面积为S，求S与a之间的函数关系式．

科目：czsx 来源： 题型：

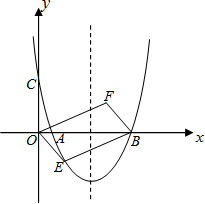如图，已知抛物线y=ax²+bx+c（a≠0）经过点A（1，0），B（6，0）和C（0，4 ）三个点．
（1）求抛物线的解析式；
（2）设点E（m，n）是抛物线上一个动点，且位于第四象限，四边形OEBF是以OB为对角线的平行四边形，求四边形OEBF的面积S与m之间的函数关系式，并写出自变量m的取值范围；
（3）当四边形OEBF的面积为24时，请判断四边形OEBF是否为菱形？

科目：czsx 来源： 题型：

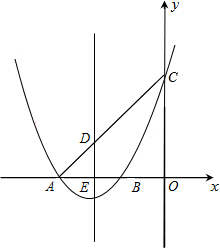如图，已知抛物线y=x²+4x+3交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，点B的坐标为（-1，0）．
（1）求抛物线的对称轴及点A的坐标；
（2）在平面直角坐标系xoy中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；
（3）连接CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．

科目：czsx 来源： 题型：

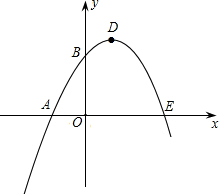如图，已知抛物线与x轴交于点A（-1，0），E（3，0），与y轴交于点B，且该函数的最大值是4．
（1）抛物线的顶点坐标是（

 

，

 

）；
（2）求该抛物线的解析式和B点的坐标；
（3）设抛物线顶点是D，求四边形AEDB的面积；
（4）若抛物线y=mx²+nx+p与上图中的抛物线关于x轴对称，请直接写出m的值．

科目：czsx 来源： 题型：

如图，已知抛物线y=x²+bx+c经过A（1，0），B（0，2）两点，顶点为D．将△OAB绕点A顺时针旋转90°后，点B落到点C的位置，将抛物线沿y轴平移后经过点C，求平移后所得图象的函数关系式．

科目：czsx 来源： 题型：

（2012•安溪县质检）如图，已知抛物线y=ax²+bx+c（a≠0）经过A（-1，0）、B（3，0）、C（0，-

3

2

）．
（1）求该抛物线的解析式；
（2）若点Q在抛物线的对称轴上，点P在抛物线上，若以O、B、P、Q为顶点的四边形是平行四边形，求所有满足条件的点P的坐标；
（3）请在抛物线对称轴上求点M，使得∠BMC=90°．

科目：czsx 来源： 题型：

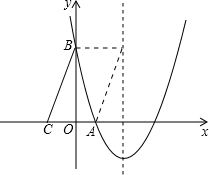如图，已知抛物线y=ax²+bx+3与x轴、y轴分别交于A（1，0）、B（0，3）两点，x轴上有一点C（-1，0），把△BOC向右平移2个单位长度后，一条直角边恰好在抛物线的对称轴上．
（1）求二次函数的关系式；
（2）把△BOC继续向右平移，当B在抛物线上时，求第二次平移的距离．

科目：czsx 来源： 题型：

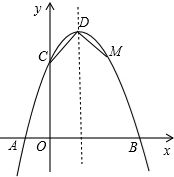如图，已知抛物线与x轴交于点A（-1，0），与y轴交于点C（0，3），且对称轴方程为x=1
（1）求抛物线与x轴的另一个交点B的坐标；
（2）求抛物线的解析式；
（3）设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；
（4）若点M是抛物线上一点，以B、C、D、M为顶点的四边形是直角梯形，试求出点M的坐标．

科目：czsx 来源： 题型：

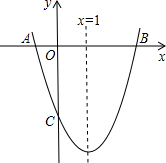如图，已知抛物线y=ax²+bx-3的对称轴为直线x=1，交x轴于A、B两点，交y轴于C点，其中B点的坐标为（3，0）．
（1）直接写出A点的坐标；
（2）求二次函数y=ax²+bx-3的解析式，并用配方法确定抛物线的顶点坐标；
（3）求△BOC的面积．

科目：czsx 来源： 题型：

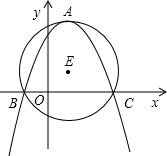如图，已知抛物线y=ax²+bx+c（a＜0）的顶点A在以E（1，1）为圆心，2为半径的圆上，且该抛物线经过⊙E与x轴的两个交点B、C，AE⊥x轴．
（1）请写出点A、B、C三点的坐标；
（2）求抛物线的解析式；
（3）在抛物线上能否找到一点P，使线段PE与OA互相平分？如果能，写出P点坐标，如果不能，请说明理由．